Solar cycle
According to the temperature in the sun, it was found that the delivery of energy from the sun is mainly the result of a number of fusion reactions, within of the so-called proton-proton cycle (abbreviated: pp-cycle). The i ndividual stages of this cycle are represented by the four nuclear equations (with the corresponding released energy):
-
The first equation
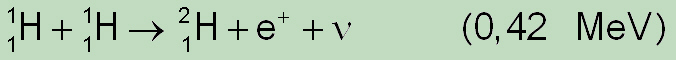
shows that the two protons are combined to produce the deuterium core (heavy hydrogen contains a proton and a neutron) in the result together with a positron (e+) and a virtually weightless "neutrino". In contrast to the photons, the Neutrinos, undisturbed on its way from the core to the surface of the sun by steady collisions, will be lost in space with the speed of light in about two seconds.
-

As shown in this second equation, positrons collide soon with the one electron, so that these two antiparticles are destroyed where their total mass is converted into energy in the form of gamma photons. The energy released can be calculated by replacing the mass of electrons and positrons in Einstein's equation,

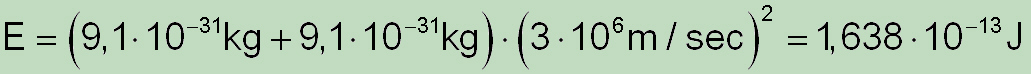
And this corresponds to 1,02 MeV (1 eV = 1.6.10-19J), as shown in the above equation.
-
In the next third stage of the pp-cycle a nucleon (proton) of the hydrogen is combined with the previously formed deuterium to form the nucleus of the third helium isotope, whereby the additional energy of gamma ray photons 5,49 MeV is released,
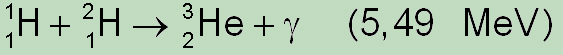
-
During the final reaction of this sequence, which is recorded in the fourth equation
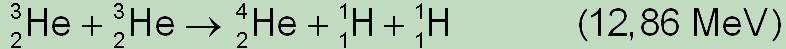
two isotopes are combined to form a stable fourth isotope of helium and two protons (hydrogen nuclei), as well to release the energy of 12.86 MeV.
As two of the third atoms of helium isotope were required for the output of the final helium nucleus, it is obvious that two at a time of the first three reactions are necessary for each response of the last fourth stage. To determine the total energy released by the overall cycle follows:
This means, the overall efficiency of the pp-cycle is that four protons are combined to produce a 42He (helium) core, two positrons, two neutrinos and two gamma rays, which after the addition of equations of all four stages can be shown
The sun produces energy at an incredible rate with the consumption of their mass, which can be seen from the calculation of the mass loss. Starting from the atomic mass unit (u), each proton has a mass of 1.0078265.u and helium nucleus (α-particles) have a mass of 4.002603.u on. After insertion in the previous equation follows
where the term in parentheses is the total energy release rate, E, that can be calculated based on the final stage by the repeated application of the Einstein equation, that is
This result is in total accordance with the value, which has been obtained by the addition of the energy from all the individual stages of the pp-cycle, as previously shown.
Based on the total energy that the sun radiates, which can be calculated on the basis of precise radiometric measurements, it has been evaluated that the number of such cycles that take place in the solar core in a second ~ 9 × 1037 are. On this ground, the total released energy is:
which is called "solar brightness" L (luminosity).
By multiplying the mass loss in a cycle with the number of cycles of 9 x 1037/s we get
This shows that every second ~ 4.3 million tones of solar mass is converted into energy. Although this amazing mass appears to be very large, it is based on the total weight of the sun from about 1.98 × 1030kg irrelevant. During its lifetime of about 10 billion years, the Sun will lose less than 0.05 percent of their initial weight at the expense of energy conversion of mass into energy.
The challenge to lend this energy to the earth is very serious and the scientists have already made great strides in this regard. Once developed, the fusion will be a virtually inexhaustible, safe, suitable for the environment and for all communities available power source.
This energy is effective and clean, almost without any consequences. Of course, the fusion processes and the materials on Earth are different from the sun, but this problem has been already resolved.
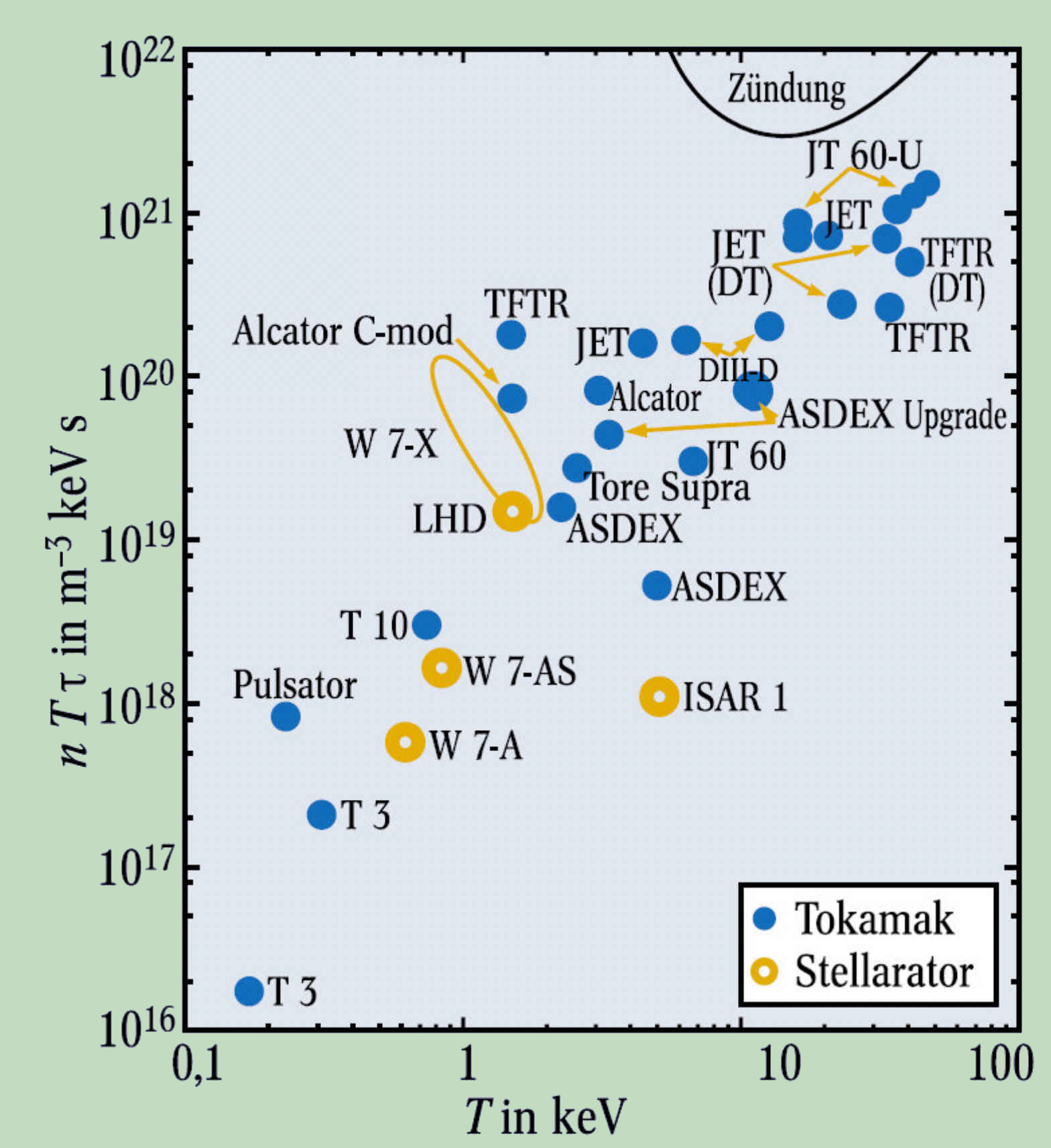
The advance of the fusion research can be best measured by the fusion product n•T•τ that is applied here against the plasma temperature T (If T is measured in energy-units, than corresponds 1 keVs to 11,6 million Kelvin). The area of the ignition (“Zindung”) in the picture corresponds to the continuous function of the facility.
Return to topBack to the "Energy"