FE-Modellierung der Schraubenverbindung unter Axiallast
Allgemeinen gesehen kann die FE-Analyse von Schraubverbindungen Vorteile in Bezug auf Zeit und Kosten gegenüber den Tests der Verbindung ergeben und ein genaueres Ergebnis bezüglich von Stress, Dehnung und Kraftverteilungen als alle anderen Methoden liefern. Allerdings wird das vorhandene Potenzial der Methode nicht immer verwirklicht, weil die Ergebnisse der Finite-Elemente-Analyse, insbesondere im Falle von Schraubverbindungen, extrem abhängig von der Modellierungstechnik sind.
Basieren an der Erkennung, dass die FE-Methode eine Annäherung an die Wirklichkeit ist, deren Erfolg von der Gewinnung von guten und insgesamt ausgewogene Entscheidungen zu verschiedenen Themen abhängt, ist es wichtig, in der Lage zu sein, ein FE-Modell zu kreieren, ohne dabei die Genauigkeit des Modells im Vergleich zu dem erforderlichen Zeitaufwand ins Frage zu stellen.
Einbeziehung der Schrauben in Finite-Elemente-Modelle simuliert reales Verhalten. Der Einfluss des Bolzens ist für das Verhalten von allen Teilen in der Verbindung entscheidend.
Vor allem während der Modellierung nimmt man wahr, wie komplex eine Schraubverbindung ist. Ausgehend von der Aufgabe der Schraubverbindungen, die verschiedenen Teile dauerhaft verbinden zu halten, also unter allen Betriebsbedingungen und Belastungen, die Eigenschaften des FE-Modells werden durch die Tatsache geleitet, dass die Schraubenverbindung eine vorgespannte Verbindung ist und nur als solche einwandfrei funktionieren kann. Die beiden Eigenschaften, Vorspannen und gegenseitige Kontakt der Teile erfordern extrem subtile Modellierung für die Zwecke der genauen FE-Analyse.
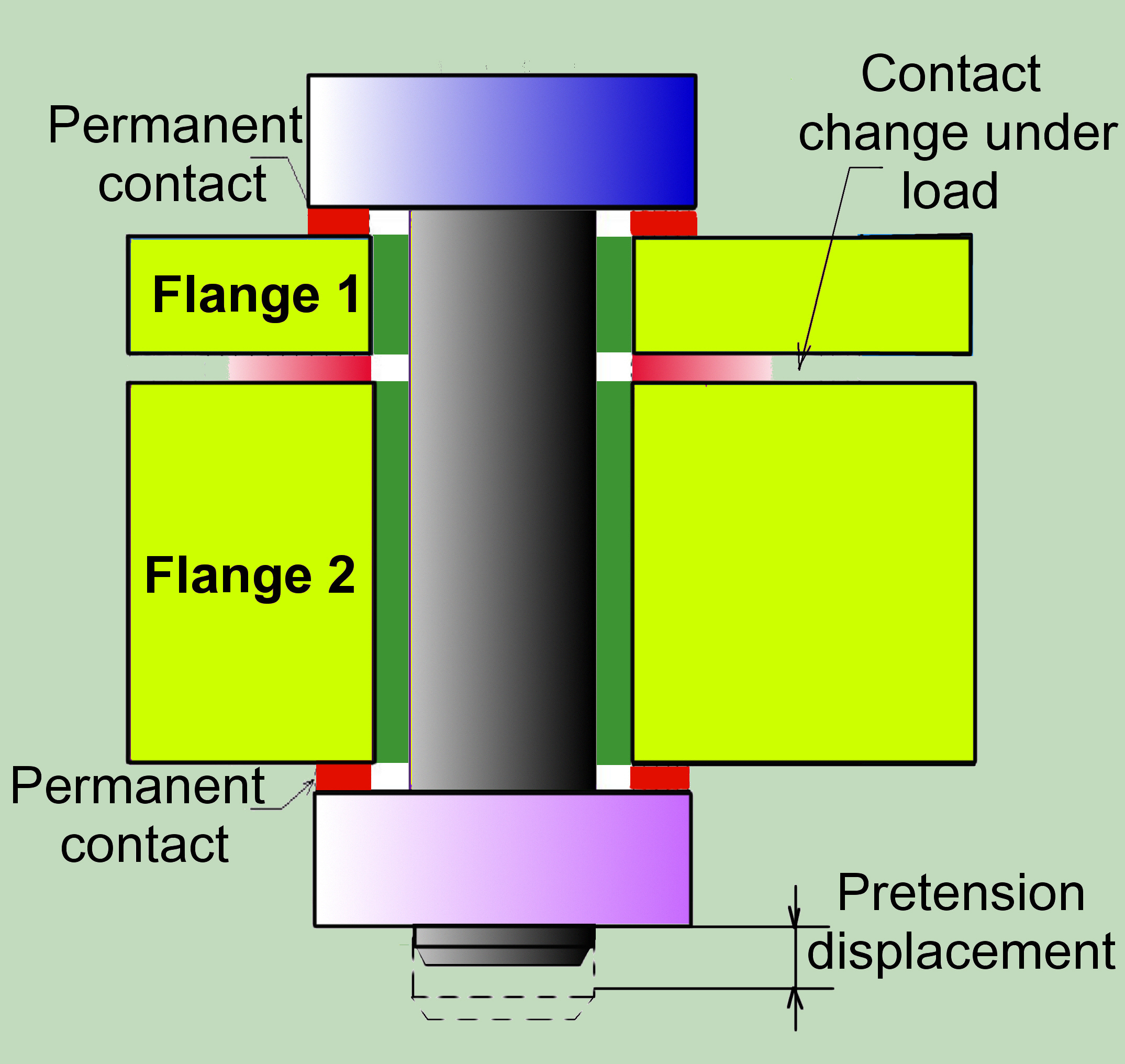
Dennoch, gerade aufgrund der gegebenen Komplexität, sind die möglichen Vereinfachungen zwingend. Die Frage ist, Welche sind möglich und tragbar.
Aus der Sicht der Simulation müssen die Oberflächen in Kontakt, die sich unter Last verändern, in der Lage sein auch sich zu trennen. Hier werden die Kontaktelemente, die in der Lage sind diskrete Kontakt zu darstellen verwendet.
Allerdings sind die Kontaktelemente in den Kontaktflächen zwischen den Flanschen und der Kopf/Mutter des Bolzens, in denen in den meisten Fällen der Permanentkontakt zu erwarten ist, nicht erforderlich. Leider ist dieser Anspruch nicht immer wahr. Wird der Querschnitt zu sehr von dem Schraubenloch geschwächt oder der Bolzen ist zu steif ein Gelenk könnte entstehen und die Schraube kann nur einseitig im Kontakt sein. Bei den querbelasteten Verbindungen mussten außerdem an diesen Stellen die Reibungsverhältnisse berücksichtigt werden. Im Allgemeinen die Nichtberücksichtigung des einen oder anderen Merkmals ist eine engineermäßige Entscheidung, die die Kenntnisse über das Verbindungsverhalten unter den bestimmten Betriebsbedingungen voraussetzt, was durch eine parallele Analyse mittels geeigneter Analyseverfahren, wie hier vorgeschlagen, erreicht werden kann.
Sowohl FE oder analytische Modellierung der ganzen Mehrschraubenverbindung ist in der Regel nicht erforderlich, womit auch nicht praktikabel und würde von den grundlegenden Aufgabenstellung ablenken. Es kann ausreichend sein, ein einzelnes Segment der verbundenen Struktur mit sorgfältig ausgewählten Randbedingungen, um die bestehende Koppelung der aktuellen Verbindung zu replizieren, zu modellieren. Das Befestigungselement ist mit Lasten, die die lokale Vorbelastung unter welchem auch komplexen ungleichmäßigen Belastungsbedingungen vorkommen zu belasten. Ausgehend von der Letzteren aber besonders darauf zu beachten, dass die Mehrschraubverbindungen statisch unbestimmt sind. Symmetrische Bedingungen als zyklische Symmetrie könnten nur dann praktiziert, wenn die beiden folgenden Bedingungen erfüllt sind: Geometrie ist symmetrisch und Randbedingungen (einschließlich der Lasten und der Grenzbedingungen) sind symmetrisch.
Wegen der lokalen Form der Verbindung, die endgültige Modellierung sollte auf Festkörperschraubensimulation basieren. Um sicherzustellen, dass das FE-Mesh fein genug ist und dass die Kontaktbedingungen angemessen gelöst sind, ist es notwendig alles zu überprüfen.
In einer FEM-Simulation der Verbindung wäre es meist überflüssig, die volle Gewindeprofil zwischen dem Bolzen und der Mutter zu modellieren. Sehr detaillierte 3D-Modelle, die diesen Effekt simulieren, sind möglich( CMC Schraube), aber sie sind extrem rechenintensiv und die Ergebnisse sind sehr empfindlich auf realen Reibungsverhältnisse und geometrische Ungenauigkeiten. Es ist sinnvoller und viel mehr bequem, Handberechnungen zu durchführen, die für Margen auf Gewinde, basierend auf Schraubenschaftbelastung (Kräfte und Momente) aus FEA Ergebnissen dienen.
Weil wir nicht modellieren können was wir nicht messen können, können einige Effekte innerhalb FEA nicht (oder nur begrenzt) berücksichtigt werden, wie z. B.: Effekte der Geometrieunvollkommenheit, primäres Setzen in der Montage, Sequenzeffekten bei der Montage von Mehrschraubenverbindungen u.ä..
Vorspannen während der Montage der Verbindung
Standardverschraubungssysteme beinhalten Schraubenvorspannung. Währen der Montage setzen wir Drehmoment ein, um die Mutter zur Schraubenvorspannung zu drehen. Theoretisch können wir, um Vorspannung zu steuern, den Winkel, um den die Mutter gedreht wird, anstatt Drehmoment zu verwenden. Schließlich, wenn wir uns die Mutter auf einer Schraube um 360º drehen, erwidert die Schraube mit einer Linearverschiebung, die genau einer Steigung der Gewinde gleich ist. Daher auch wenn wir über Vorspannkraft sprechen, was wir tun, ist die Einführung der Vorspannugsverformungen durch Drehen der Mutter entlang der Bolzengewinde.
In echtem Leben, die Verbindungselementen müssen nicht unbedingt flach sein, und es kann eine gebogene Scheibe da sein, sodass die Ausgangsposition für die notwendige Umdrehung, auch zwischen scheinbar identischen Schrauben oder Verbindungen, unvorhersehbar variiert. Bei einer FEM-Simulation müssen wir uns darüber keine Sorgen machen. Es ist jedoch von entscheidender Bedeutung für die Art der Vorspannung diese durch die Einführung der Dehnungen in den zusammenhängendes System Schraube-verspannte Teile zu realisieren. Es sollte nicht überraschen, dass eine der zuerst vorhandenen Methoden, um dies in FEA zu realisieren war durch thermische Kontraktion der Schraubenschaft.
Um die Vorspannung zu aufbringen, müssen wir die Beziehung zwischen der Verschiebung und der erforderlichen Vorspannkraft wissen und der geeigneten Position für die Einführung dieser Verschiebung auswählen.
Die Verformungen in einer Verbindung kann dem sog. Verspannungschaubild entnommen werden.
Verspannungschaubild ist eine populäre und nützliche grafische Darstellung des Verhaltens von Schraubenverbindungen, und zeigt die Beziehungen zur Außenbelastung, Schrauben- und Platten-Steifigkeiten, Schraubenkraft, Klemmkraft in der Fuge, und das Abheben der Verbindung.
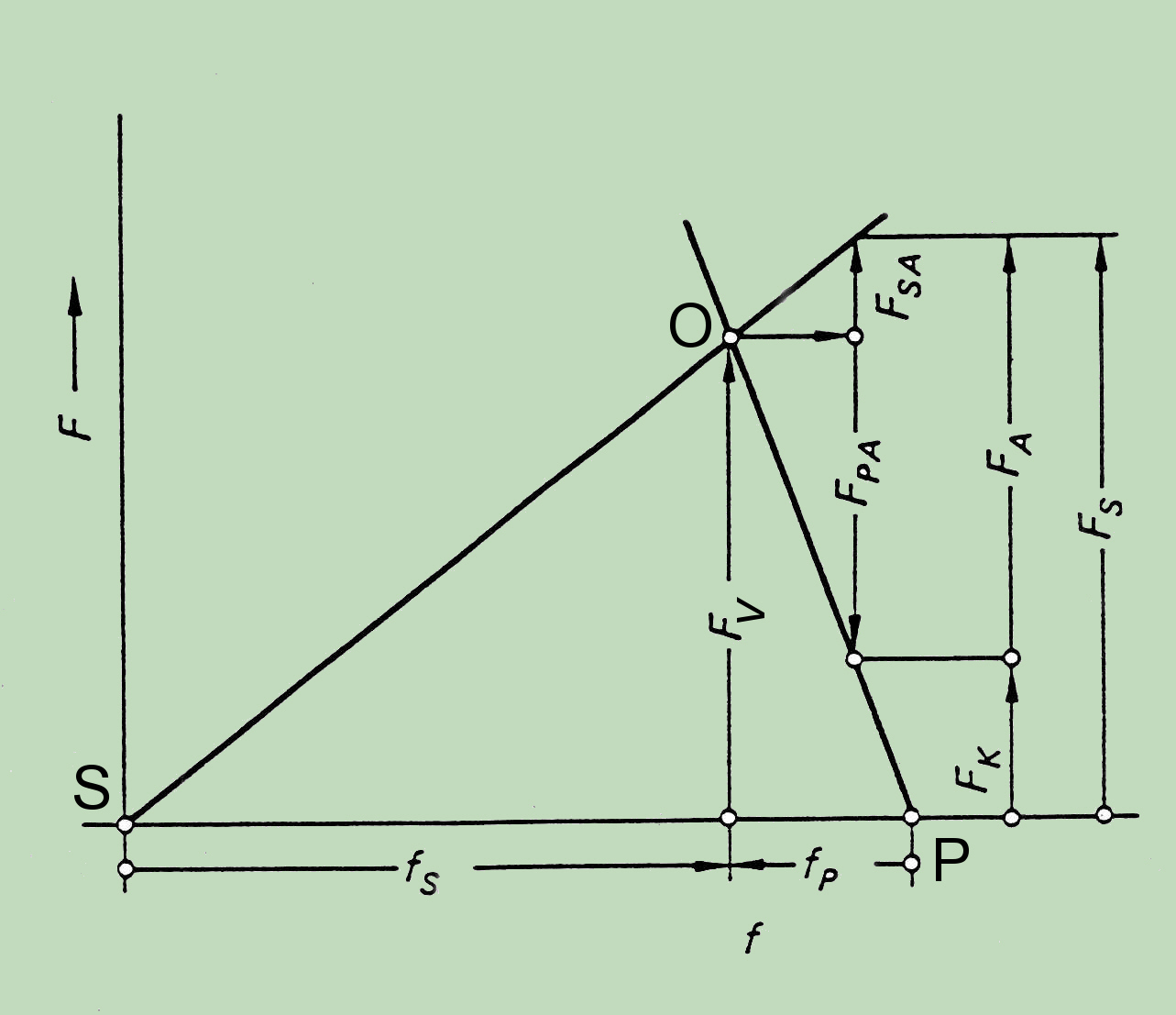
Die Beziehung zwischen der Vorspannung der Verbindung und der Dehnung der Schaube ist durch die Schraubenkurve dargestellt, die nichts anderes als die Federkennlinie des Schraubebolzens ist. Die Steigung dieser Linie ist abhängig von Material und Geometrie. Wenn die Schraube angezogen wird, verlängert sich der Bolzen entlang der Linie SO um fS (siehe Abbildung). Die Reaktionskraft (die rechte Seite der Grafik) ist die Klemmkraft der Verbindung und die Verbindung wird zusammengedruckt, wie die Linie PO zeigt, für fP. In diesem Beispiel ist die Bolzenspannung äquivalent zu der Vorspannung, die der Kompressions der Verbindung entspricht. Deshalb ist die Verformung der Verbindung, die durch Drehen der Mutter realisiert wird, erforderlich für die gewünschte Vorspannkraft, die Summe fS + fP.
Diese verändert sich nach der Einführung der äußeren Kraft. Wenn eine konzentrische Außenlast FA unter dem Schraubenkopf und der Mutter (gleiche Bild) appliziert wird, verlängert sich der Bolzen um einen zusätzlichen Betrag, während die zusammengepresste Verbindungselementen teilweise entlastet werden. Diese gekoppelte Veränderung der Verformung mit äußeren Kraft ist der Schlüssel für die Wechselwirkung der Kräfte in Schraubverbindungen. Die Ergebnisse der FEA werden nur dann adäquat, wenn diese Wechselwirkung der Kräfte unter allen Bedingungen aufrechterhalten wird.
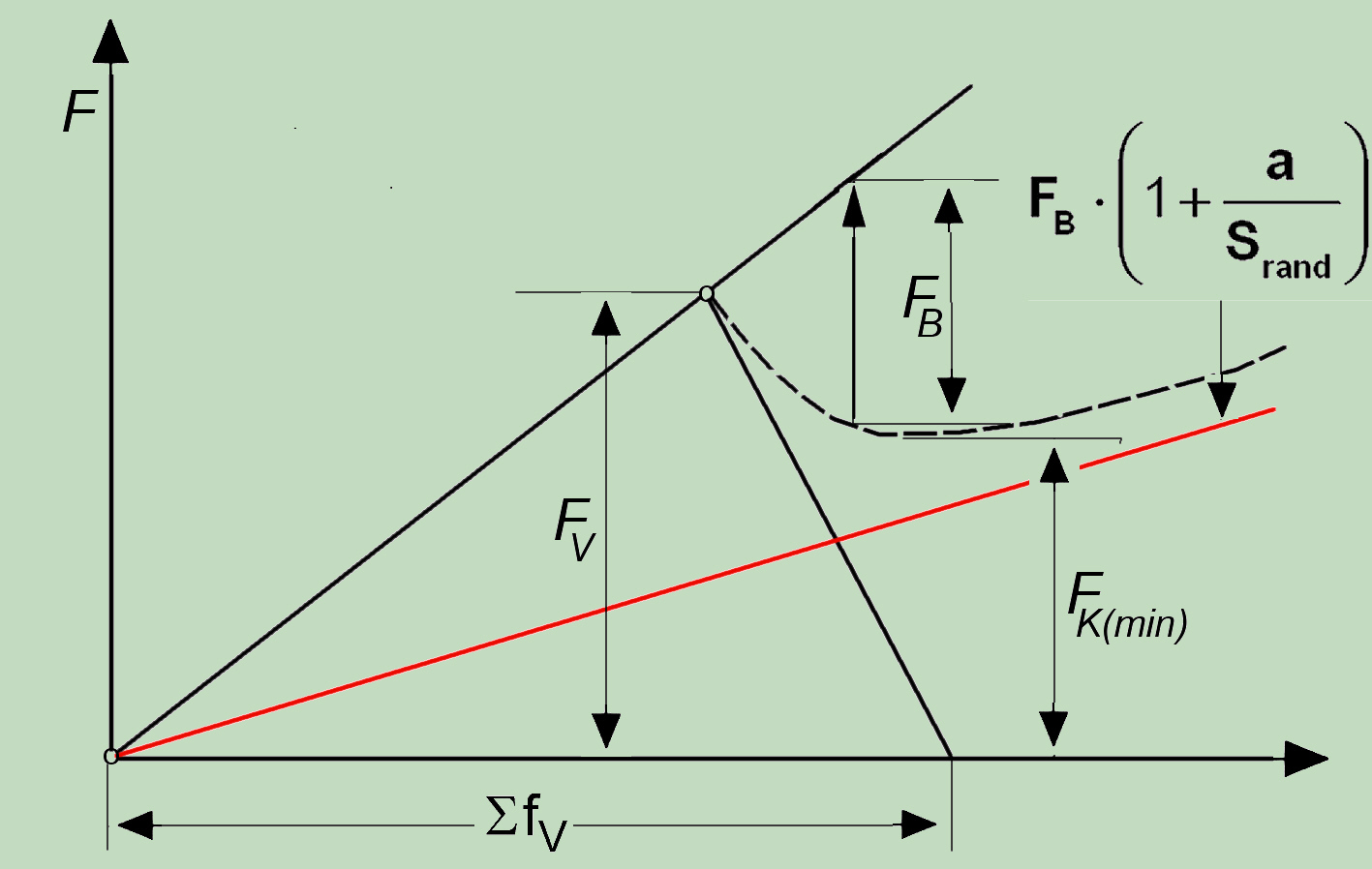
Bei exzentrischer Belastung Verbindung ist die Situation, allerdings viel komplexer als durch dieses einfache Verspannungschaubild gezeigt. Durch die exzentrische äußere Kraft wird auch die Reaktionskraft in der Fuge bis zum Rand getrieben, sodass hier die Hebelwirkung entsteht (rot in der Abbildung) die zu der erheblichen Überlastung der Verbindungsschraube führt. Nach dem erreichen von FK(min) funktioniert die Verbindung nicht mehr und alle Teile werden überproportional belastet.
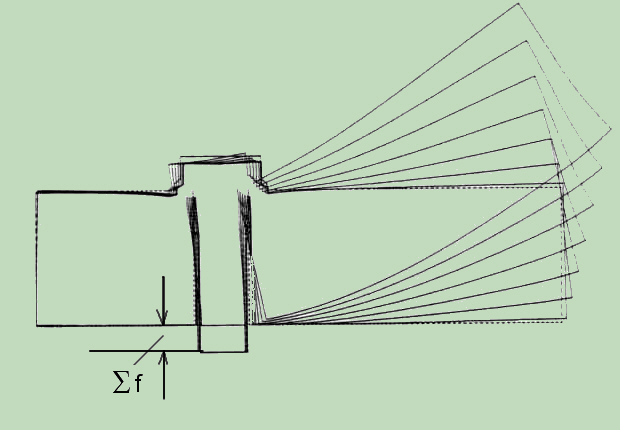
Wenn, basierend an der Symmetrie, nur eine Hälfte der Verbindung modelliert wird, ist die Einführung die Vorspannungsverschiebung, wie in der Figur gezeigt ist, relativ einfach. Die Vorspannung wird durch eine Anfangsdehnung des Bolzenanteils gegen die Symmetrielinie realisiert. Das Bild zeigt auch, wie die Anfangsdehnung für alle Stufen der Belastung der Verbindung unverändert bleibt.
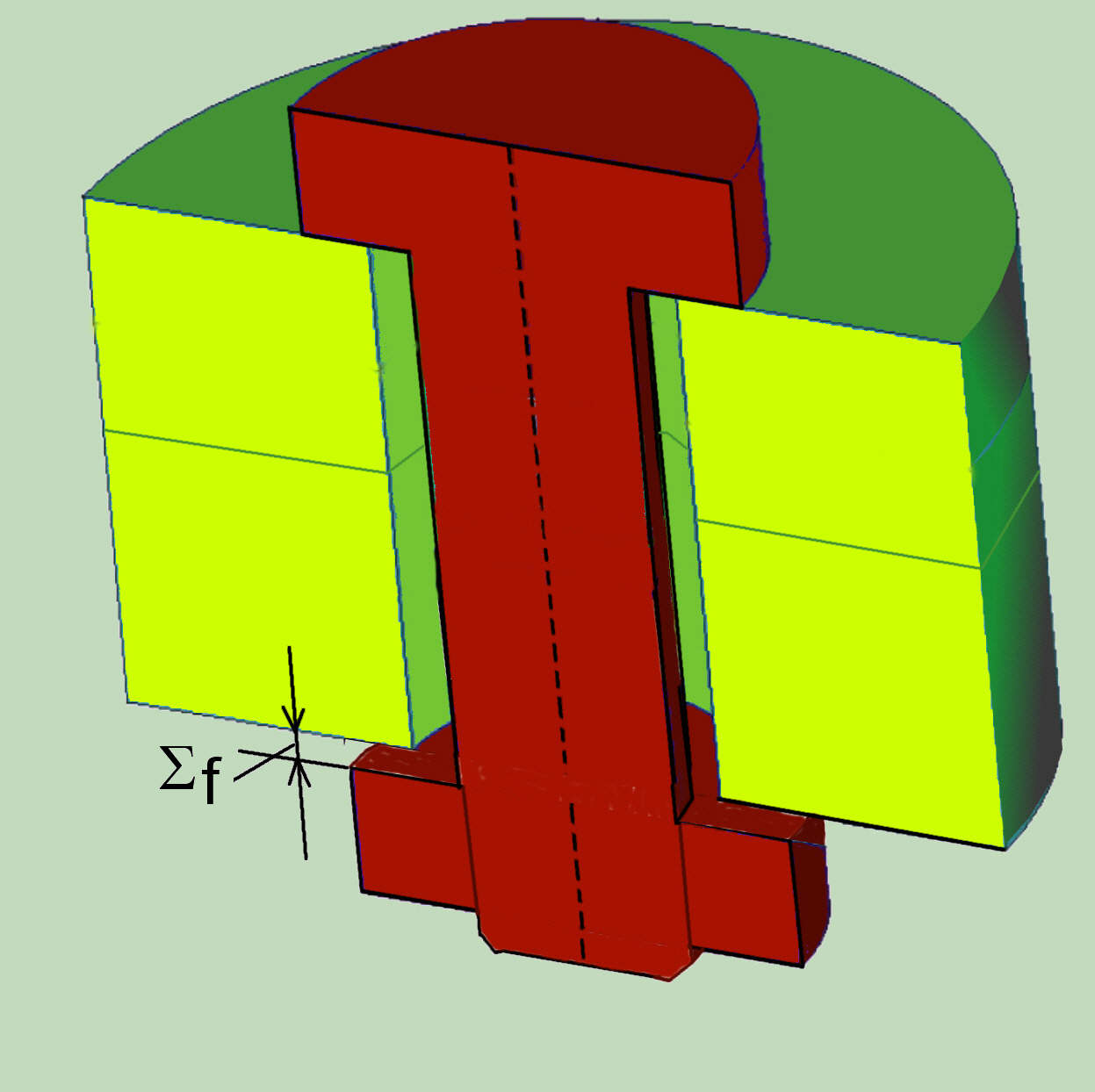
Für die komplexen Verbindungsmodelle, die Vorspannung kann in der Regel mit Randbedingungsgleichungen oder einer besonderen Form der Knotenkoppelung modelliert werden. Anstelle der direkten Kopplung der Knoten werden Gleichungen verwendet, die zwischen den zugeordneten Knoten die Erstellung einer beständigen anfänglichen Dehnung des Schraubenschaftes simulieren. In einigen FEM (MARC, ABAQUS) sind die derartigen Randbedingungsprozeduren (TYING) für den Benutzer automatisiert.
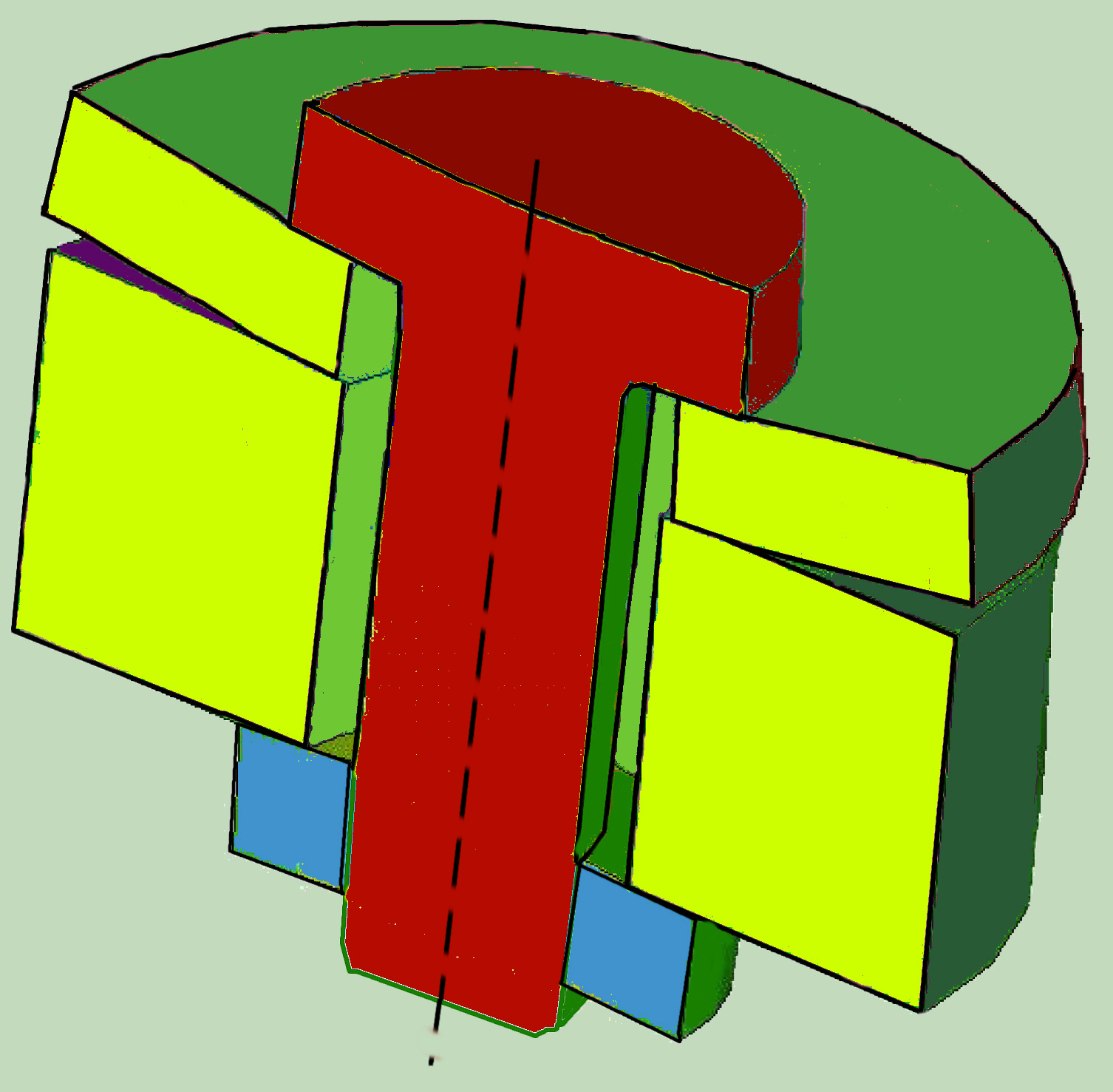
In diesem Fall wird die Oberfläche (d. h. alle Knoten) im Kontakt zwischen dem Schraubenkopf oder der Mutter und die verbundenen Platten gekoppelt sein. Dies kann als die Einführung an dieser Stelle einer unendlich steifen Scheibe, der Dicke von der Vorspannungsdehnung, veranschaulicht werden.
Einige FE-Software verfügen bereits über ein integriertes Tool zur Simulation der Schraubenvorspannung.
Bei zylindrischen Verbindung, besonders, wenn die Dicke einer der verbundenen Teile geringer ist, kann die Trennung zwischen den Oberflächen in Kontakt auch während der Vorspannung möglich sein. Dies wird ferner die axiale Steifigkeit der Verbindung reduzieren.
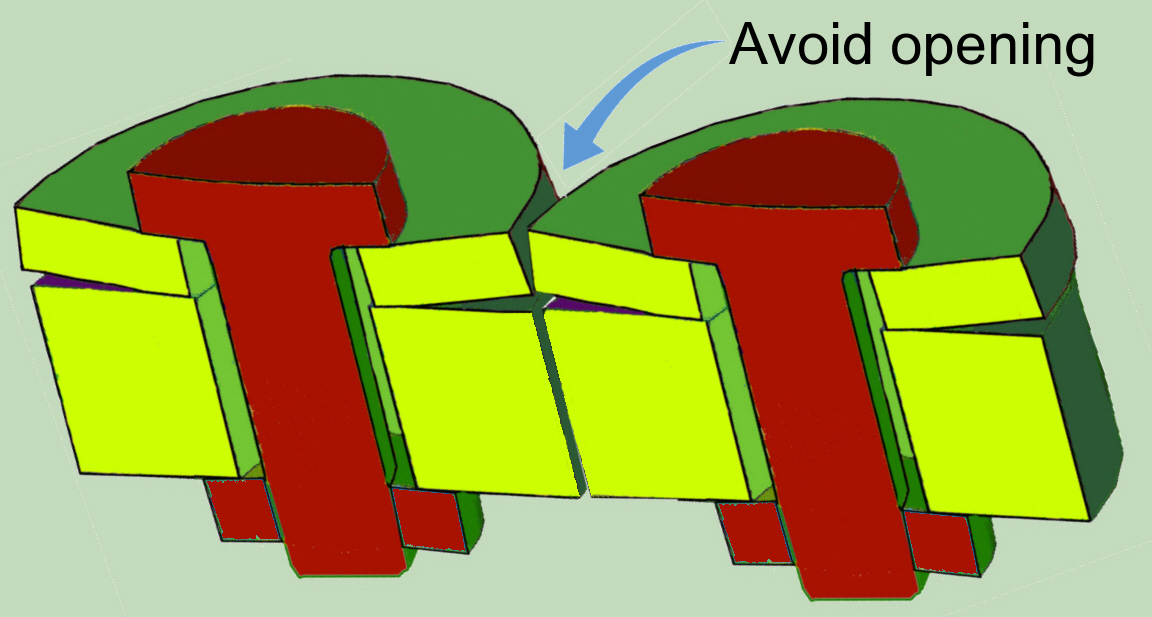
Wenn jedoch nur einen Sektor der der Mehrschraubenverbindung modelliert wird, muss dieses Verhalten an den Grenzen zu dem benachbarten Sektor durch die angemessenen Grenzbedingungen unterdrückt werden, damit die kontinuierlichen Verschiebungen gewährleistet werden.
Schließlich, im Falle von Mehrschraubenverbindungen, wenn nur die Modellierung des am meist belasteten Sektor verwendet wird, sollte nicht vergessen werden, dass die globale Belastungsumverteilung von Deformationen abhängt, die nicht-linear sind und daher auch nicht-linear sein wird.
Typische Formeln, wie zum Beispiel für Flansch oder Plattenabdeckung und ähnliches,
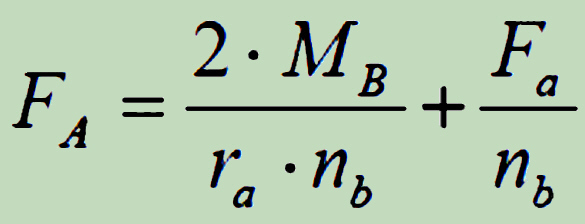
hat, obwohl in der Regel auf der sicheren Seite, keine universelle Anwendung und sollte durch die weiteren Untersuchungen überprüft werden.
Return to top
Zurück zu den Schraubenverbindungen