Realen Konstruktionen verhalten sich unter kritischen Lastbelastungen in der Regel auf eine nicht-lineare Weise. Unter diesen Bedingungen kann eine lineare Lösung zu fehlerhaften Ergebnissen führen. Für die modernen Konstruktionen ist die Herausforderung analytische Werkzeuge und Baumodelle zu entwickeln, die es auch unter diesen Bedingungen möglich machen, die Analyse der Strukturintegrität mit einem ausreichenden Vertrauensgrad zu durchführen. Darüber hinaus ist das wichtige Ziel der nicht-linearen Analyse das Verstehen des Verhaltens von Bauteilen der Struktur bei den veränderlichen Arbeits- und Belastungsbedingungen (und nicht nur das Erfüllen von Code-vorgeschriebenen Begrenzungen).

Klassische Analyse-Techniken werden auf vereinfachten linearen Annäherungen gegründet. Beinahe alles von der Mathematik und der Wissenschaft, mit dem wir gegenwärtig vertraut sind, wird in einer linearen Form präsentiert - das heißt, die Endergebnisse der Gleichung variieren in direktem Verhältnis zur Eingabe. Dies scheint uns sehr natürlich, weil wir nicht-linearen Wachstums aus Natur und Alltag nicht immer bewusst sind. Deshalb nehmen wir abermals für sicher, dass die Welt so funktioniert - wie ein Ball, der zweimal so hart gestoßen wird, auch zweimal schneller geradlinig in gewünschter Richtung fliegen wird (das sollen sie einem Fußballer beibringen) .
Alle diese Modelle des Verhaltens sind einfach und verlangen zur Berechnung womöglich weniger Verarbeitungszeit, aber im Allgemeinen - sind sie fortwährend falsch. Doch, wir beharren auf dessen Ausübung, teilweise, weil wir wissen, wir haben eine ganze Menge von angesammelter Erfahrung und Werkzeugen, die an den linearen Systemen basieren. Deshalb sehen wir gern die Weltzusammenhänge als seien sie linear. Wenn dies dann nicht wahr wäre, hätten wir große Schwierigkeiten im Vorhersagen von etwas?
Aber, das Beharren bei einem falschen wissenschaftlichen Paradigma fordert unvermeidlich einen bestimmten Preis und unter diesem fahlen auch die Misswirtschaft von unseren Ressourcen und die Fehlkalkulation von extremen Ereignissen.

In Übereinstimmung mit dem obigen Titel, wenngleich als eine Überraschung für viele, stellt sich die Tatsache, dass in der Natur nichts wirklich in einer völlig linearen Form lauft ! Abhängigkeiten in den natürlichen Strukturen sind vielfältig, komplex und verlangen die adäquaten Ingenieurproblemlösungen, die das auch berücksichtigen. Linearität ist bloß eine Annäherung.
Demzufolge ist das "lineare" im wissenschaftlich-technischen Denken nicht nur eine unzureichende Interpretation des Umgebungsgeschehens, sondern deutet auch auf, dass die derartige Verfahrensweise zunehmend mit der "nicht-linearen" Natur in einem Konflikt geriet.
Im Ergebnis, trotz des offensichtlichen Erfolges der Annahme von Linearität in der Konstruktionsanalyse, erfordern die unzähligen Probleme in der Praxis die Berücksichtigung von nicht-linearem Verhalten. Insbesondere bringt die Tragfähigkeitsanalyse von Strukturen neben dem nicht-linearen Verhalten von Materiellen, manchmal auch die geometrischen Nicht-Linearitäten in Spiel. Im Großen und Ganzen, die Untersuchung von Strukturintegrität ohne Berücksichtigung des nicht-linearen Verhaltens ist in den meisten Fällen unzureichend.
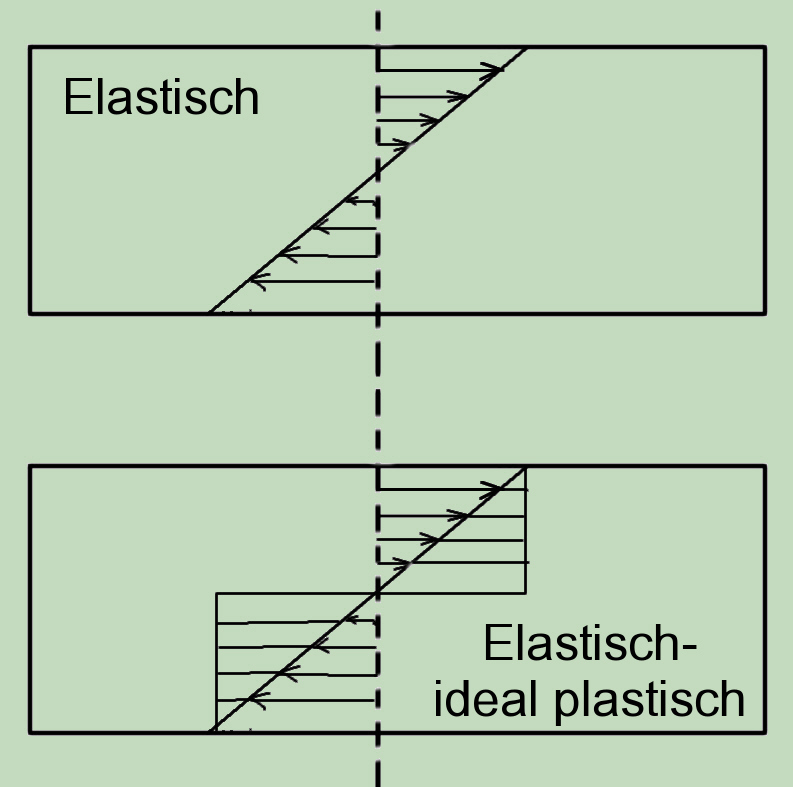
Unter einer Biegebelastung entstehen im Querschnitt einer Schale oder Balken Zug- und Druckspannungen, die ihre Maximalwerte am Rand des Querschnitts erreichen. Da die Verteilung der Spannungen linear ist, geht sie in der Mitte durch Null und die Spannungsverteilung auf der Zug- und Druckseite hat die Form eines Dreiecks. Wenn an den Rendern Fließgrenze erreicht ist verändert sich die Verteilung. Für einen elastisch-ideal plastischen Werkstoff werden die inneren Schichten des Werkstoffes immer mehr zum Tragen (bis zum Erreichen der Fließgrenze) gebracht. Die zusätzlichen Spanungen bauen einen Quadrat gleicher Größe (die Höhe entspricht Fließgrenze), wobei aber ihr Gewichtspunkt nur eine Hälfte des elastischen Spannungsdreiecks beträgt. Somit erhöht sich die Tragfähigkeit durch die plastischen Verformungen mit dem Faktor K = 1.5. Natürlich ist diese nur möglich, wenn sich der Werkstoff „unbegrenzt“ plastisch Verformt.
Tatsächlich ist die Festigkeit gegenüber Biegung höher als gegenüber Zugbelastung aber die Verhältnisse sind viel komplizierter. Die meisten Werkstoffe sind im plastischen Bereich verfestigend, ihre Dehnungskapazitäten sind begrenzt, die Biegung wird durch Querkräfte begleitete und, und ...
Die Konstruktionsmethode muss zu einer in technischer und wirtschaftlicher Hinsicht guten Lösung führen. Dabei muss sie auch die Voraussetzungen schaffen, die ein Erkennen und Berücksichtigen von funktionellen und wirtschaftlichen Abhängigkeiten und Beeinflussungen zwischen den Elementen der Konstruktion und den Faktoren der Produktion ermöglichen. Zunehmende Komplexität der Produkte aufgrund steigender Anforderungen an ihre technische Leistungsfähigkeit und Qualität ist auch ein Grund, dass die Entwicklung von Konstruktionsmethoden heute bei Wissenschaft und Praxis ein besonderes Anliegen ist. Diesbezüglich gewinnen heute bei sozio-ökonomisch-technischen Prozessen Vorgehensweise und Methoden der Systemtechnik ("System Engineering") zunehmend an Bedeutung. Die Systemtechnik als interdisziplinäre Wissenschaft will Methoden, Verfahren und Hilfsmittel zur Analyse, Planung, Auswahl und optimalen Gestaltung komplexer (in der Regel nicht-linearen) Systeme bereitstellen.
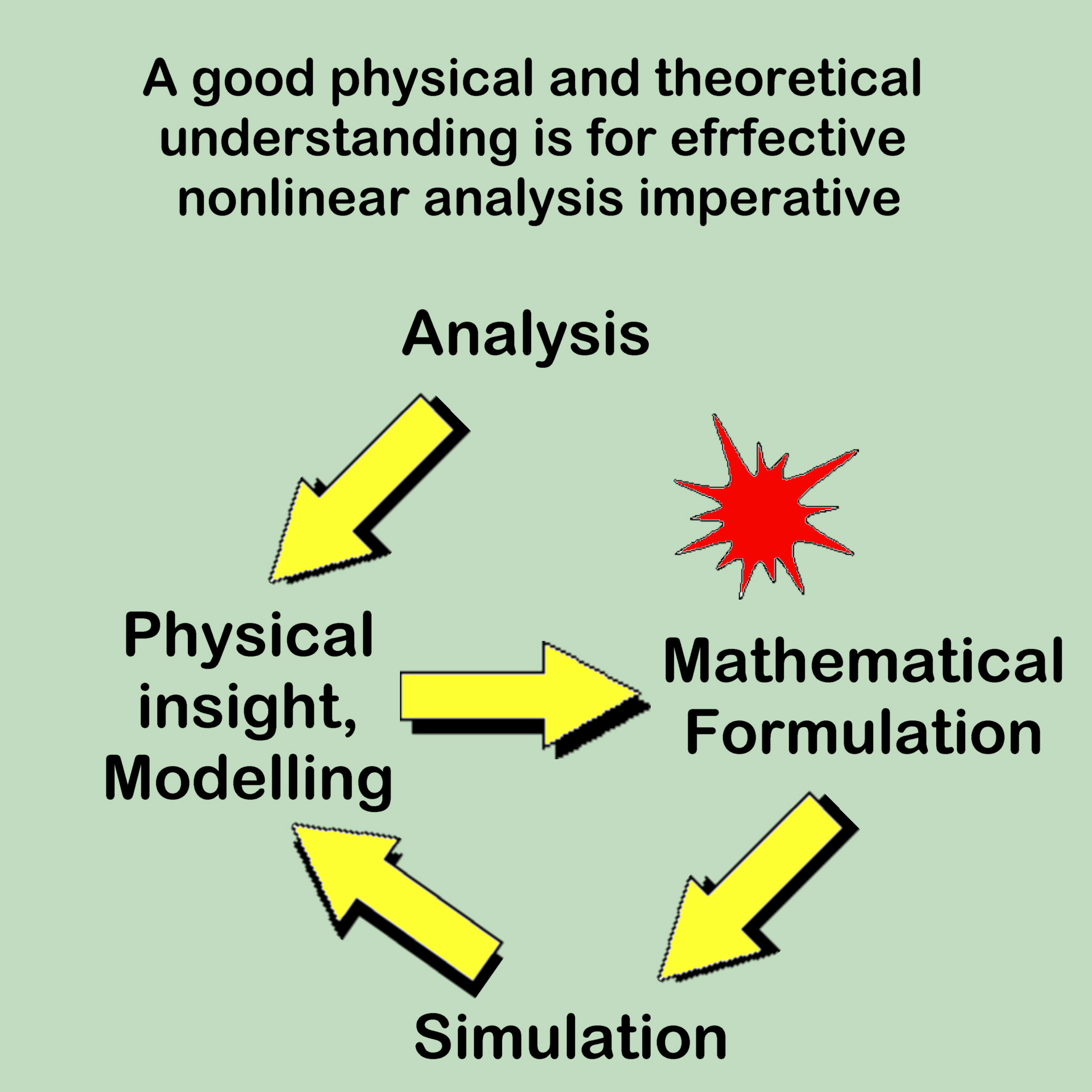
Investieren von mehr Ressourcen zur Entwicklung von Methoden und Werkzeugen, die nicht nur diese komplexe Wirklichkeit anerkennen, sondern auch diese tatsächlich einbeziehen, ist unumgänglich. Wir sollen dabei zwei getrennte, aber verwandte Probleme unterscheiden, die in wissenschaftlicher Analyse vorkommen. Das Anfang-Problem beinhaltet das, was wir einzig und allein Modellierung nennen: Wie können wir, für einen Prozess gegeben in der "wirklichen" Welt, die beste mathematisch-physische Beschreibung oder das Modell erzeugen? Das Zweite ist rein mathematisch: Gegeben sind die Gleichungen, was sind ihre Eigenschaften, und wie können diese gelöst werden? Die Lösungergebnisse sind die Voraussage der Antworten nicht-linearen Strukturen auf die, zum Beispiel, Belastung von außen. Als Ingenieure wollen wir, sowohl die wirkliche Welt modellieren als auch imstande sein, die resultierenden Modelle zu lösen, und deshalb müssen wir beide Probleme ins Auge fassen, weil das Zusammenspiel zwischen ihnen entscheidend ist.
Historisch gesehen, allerdings waren Ingenieure wegen der komplexen Problemformulierung und langen Lösungszeiten unwillig die nicht-lineare Analyse zu berücksichtigen. Die dadurch entstandene Lücke wurde dann durch praktischen Erfahrungen, höhen Sicherheitsfaktoren u. dgl. kompensiert. Das verändert sich heute, als die nicht lineare Software mit CAD kommuniziert und dadurch viel leichter zu benutzen ist. Außerdem haben verbesserte Lösungsalgorithmen und mächtige Desktop-Computer Lösungszeiten gekürzt.
Vor einem Jahrzehnt erkannten die Ingenieure die Computer-Software als ein wertvolles Design-Werkzeug. Jetzt beginnen sie, die Nutzen und größere Sachkenntnisse zu erkennen, dass nicht-linearer Ansatz und die korrespondierende Software zum Designprozess beitragen. Machen Sie auch mit!
Das Überlagerungsprinzip kann nicht angewandt werden. So, zum Beispiel können die Ergebnisse mehrerer Lastfälle nicht kombiniert werden. Ergebnisse der nicht-linearen Analyse können zu dem Zweck auch nicht skaliert werden.
Nur ein Lastfall oder Lastfallkombination kann zu gleicher Zeit gehandhabt werden.
Die Reihenfolge von Lasten (die Belastungsgeschichte) kann wichtig werden. Besonders sind die plastischen Verformungen davon abhängig.
Der Ausgangsspannungszustand (Vorspannung und Restspannungen) können bedeutend werden.