Real designs typically behave in a non-linear manner under critical loads. Under these conditions, a linear solution can produce erroneous results. For modern constructions, the challenge is to develop analytical tools and construction models that make it possible to analyse the structural integrity with a sufficient degree of confidence even under these conditions. In addition, the important goal of non-linear analysis is to understand the behaviour of components of the structure under the changing workings and loading conditions (and not just the fulfilment of code-prescribed limits).

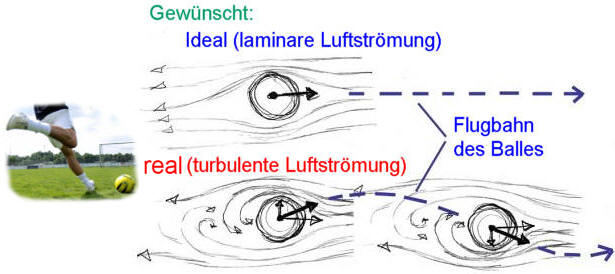
Classical analysis techniques are based on simplified linear approximations. Almost all of the mathematics and science, that we are currently familiar with, is presented in a linear form - that is, the end results of the equation vary in direct proportion to the input. This seems very natural to us because we are not always aware of non-linear growth from nature and everyday life. That is why we once again take for granted that the world works like this - like a ball that is hit twice as hard, will also fly twice faster in a straight line in the desired direction (You should try to teach a footballer about that….).
AAll of these models of behaviour are simple and may require less processing time to compute, but in general - they are steadily wrong. Yet, we persist in practicing it, in part because we have a fair amount of accumulated experience and tools based on the linear systems. That is why we like to see the world as if it were linear. If this were not true, would we have great difficulty predicting something?
However, the insistence on a false scientific paradigm inevitably requires a certain price, and below that the mismanagement of our resources and the miscalculation of extreme events pale.

In keeping with the title above, albeit a surprise to many, there is the fact that nothing in nature actually runs in a completely linear fashion! Dependencies in natural structures are diverse, complex and require adequate engineering problem solutions that also take this into account. Linearity is just an approximation.
Therefore, the 'linear' in scientific-technical thinking is not only an inadequate interpretation of what is happening in the surroundings, but also indicates that such a procedure increasingly came into conflict with 'non-linear' nature.
In summary, despite the apparent success of the linearity assumption in design analysis, the myriad problems in practice require consideration of non-linear behaviour. In particular, the load-bearing capacity analysis of structures brings not only the non-linear behaviour of materials into play, but sometimes also the geometric non-linarites. By and large, studying structural integrity without considering nonlinear behaviour is inadequate in most cases.
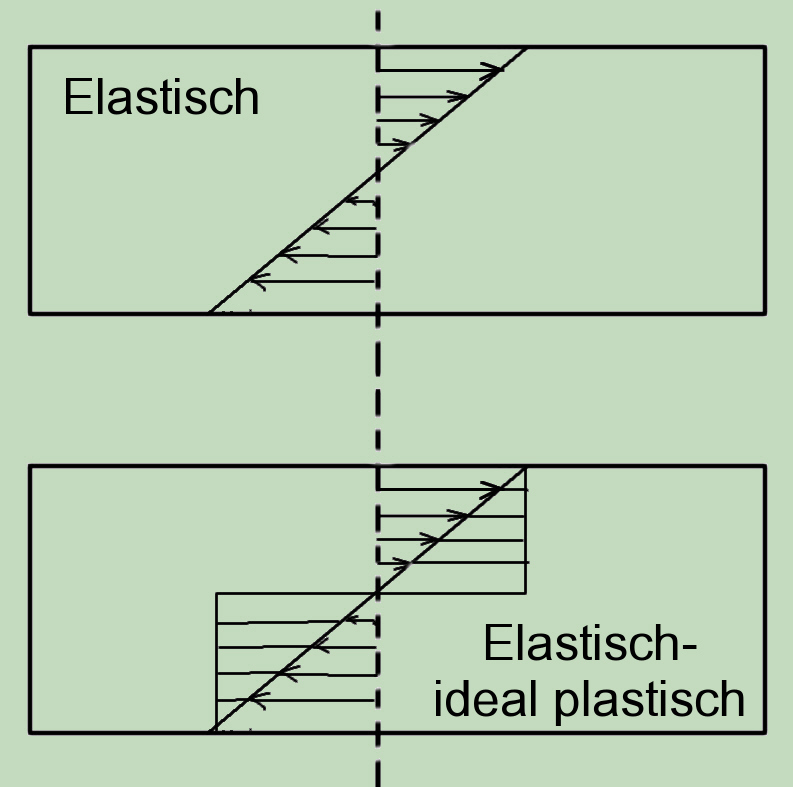
Under a bending load, tensile and compressive stresses arise in the cross-section of a shell or beam, which reach their maximum values at the edge of the cross-section. Since the distribution of the stresses is linear, it goes through zero in the middle and the stress distribution on the tension and compression side has the shape of a triangle. When the yield point is reached at the rendering, the distribution changes. For an elastic, ideally plastic material, the inner layers of the material are brought to bear more and more (until the yield point is reached). The additional stresses build a square of the same height (the height corresponds to the yield point), but their weight point is only one half of the elastic stress triangle. Thus, the increase in the load-bearing capacity due to the plastic deformation increases with the factor . K = 1.5. Of course, this is only possible if the material undergoes “unlimited” plastic deformation.
In fact, the strength against bending is higher than against tensile loading, but the situation is much more complicated. Most materials harden in the plastic range, their expansion capacities are limited, the bending is accompanied by transverse forces and, and ... .
The design method must lead to a good solution from a technical and economic point of view. In doing so, it must also create the conditions that enable the recognition and consideration of functional and economic dependencies and influences between the elements of construction and the factors of production. The increasing complexity of the products due to increasing demands on their technical performance and quality is also one reason that the development of construction methods is a special concern of science and practice today. In this regard, the procedures and methods of system engineering ('System Engineering') are becoming increasingly important in socio-economic-technical processes today. Systems engineering as an interdisciplinary science aims to provide methods, processes and aids for the analysis, planning, selection and optimal design of complex (usually non-linear) systems.
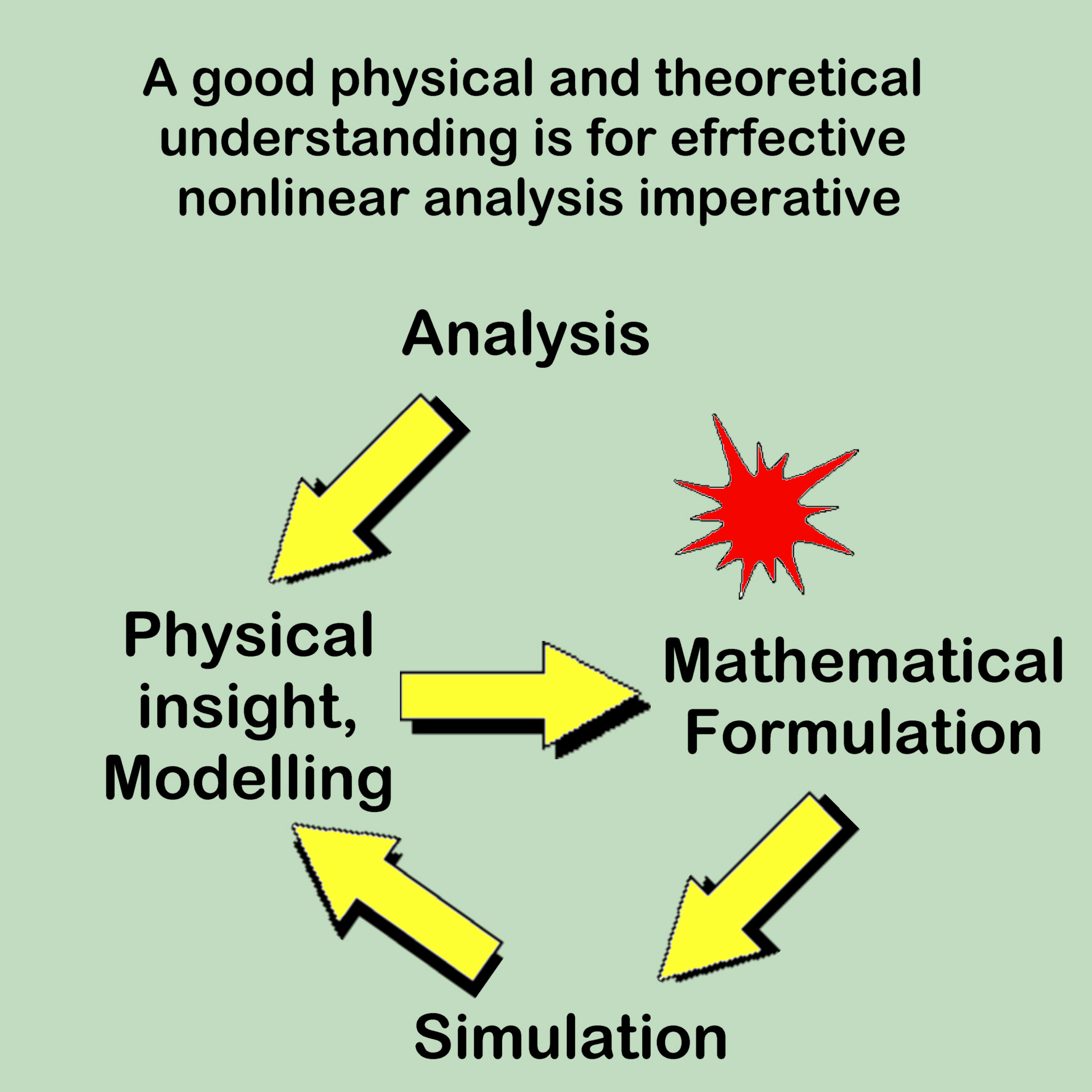
Investing more resources to develop methods and tools that not only recognize this complex reality, but actually incorporate it, is essential. We should distinguish between two separate but related problems that arise in scientific analysis. The beginning problem involves what we solely call modelling: Given a process in the “real” world, how can we write down the best mathematical-physical description or model? The second is purely mathematical: the equations are given, what are their properties, and how can they be solved? The solution results are the prediction of the responses to non-linear structures to, for example, external stress. As engineers, we want to both model the real world and be able to solve the resulting models, and so we need to look at both problems because the interplay between them is crucial.
Historically, however, engineers were unwilling to consider non-linear analysis because of the complex problem formulation and long solution times. The resulting gap was then covered by practical experience, high safety factors and the like. That changes today when the non-linear software communicates with CAD and is therefore much easier to use. In addition, improved solution algorithms and powerful desktop computers have shortened solution times.
A decade ago, engineers recognized computer software as a valuable design tool. Now they are beginning to see the utility and greater expertise that the non-linear approach and corresponding software add to the design process.
Please, take part in this development also!
All real-world designs behave in a non-linear way at a certain load level. In a few cases, a linear analysis may be appropriate. In many other situations, a linear solution can produce erroneous results because the assumptions made are much more complicated.
Of course someone will put the question: What do I get out of it? Especially since the effort is much greater.
As the example of the bending above shows, the non-linear behaviour often conceals considerable reserves, so that the non-linear behaviour can lead to a significant increase in capacities. In the other cases it is exactly the opposite. Observing behaviour during the analysis (whether failure or life) is perhaps more important than a rigorous quantitative assessment of the maximum load or deformation observed. One of the most important goals of the non-linear analysis should therefore become the understanding of the behaviour and not just the fulfilment of code-prescribed limits.
The superposition principle cannot be used. For example, the results of several load cases cannot be combined. Results of the non-linear analysis cannot be scaled for this purpose either.
Only one load or loads cobination case can be handled at the same time.
The sequence of loads (loading history) may become very important. Particularly, plastic deformations depend on it.
The initial state of stress (preloading and residual stresses) may be significant.