Im Allgemeinen kann das Versagen von Bauteilen in Ingenieurstrukturen und der Strukturen selbst meistens auf Oberflächenrisse zurückgeführt werden. Besonders bei dünnwandigen Teilen der Strukturen ist das Versagen des Ligamentes, das zum Wanddurchbruch führt, die Hauptursache für das Versagen der Struktur. Der kritische Querschnitt wird durch das Vorhandensein des Oberflächenrisses, trotz seiner kleinsten Dimension, entscheidend geschwächt und ist deshalb stets für das Versagen verantwortlich. Die Untersuchung der Beziehungen für die Ermittlung der Grenzlast einer Struktur mit dem Oberflächenriss ist deshalb eine wichtige Aufgabe im Rahmen der zuverlässigen Bruchvorhersage.
Bestimmung der Restfestigkeit für Bauteile mit dem Oberflächenriss
-
Im 1976 wurde basierend an dem sogenannten Strip Yield Model, das ausgehend von der Platte mit dem Durchgangsriss entwickelt ist, die R6 Methode eingeführt (bekannt auch als FAD = Failure Assessment Diagramm). Sie wurde von SINTAP (Structural Integrity Assessment Procedures for European Industry) auch auf den Fall der Strukturen mit den Oberflächenrissen übertragen. Leider gibt es keine theoretischen oder empirischen Beweise für die Gültigkeit dieser Losung für die Oberflächenrisse. Zahlreiche experimentelle Ergebnisse zeigen einen signifikanten Unterschied im Verhalten der Proben mit Oberflächen- und Durchgangsriss, weswegen sogar in USA eine gesonderte Norm für die Bestimmung von KIe (ASTM-E-740) eingeführt wurde.
-
Unsere experimentellen Ergebnisse, im Rahmen von den von ESA (European Space Agency) finanzierten Vorhaben, haben einen maßgebenden Unterschied im Verhalten der Proben mit Durchgangs- und Oberflächenriss gezeigt. Für die Behandlung von Oberflächenrissen wurde deshalb ein neues Verfahren entwickelt und für die Auslegung des Feststoffsbusters für die zuverlässigste Trägerrakete der Welt ARIANE 5 erfolgreich verwendet.
-
Hierfür ist im Besonderen verkomplizierend, dass sowohl die Spannungsintensität als auch die Dehnungsbehinderung entlang der Kontur der Oberflächenrisse ungleichmäßig ist, wobei sich diese Ungleichmäßigkeit unter den elasto-plastischen Belastungsbedingungen durch die unterschiedlichen örtlichen Fließbedingungen noch weiter verstärkt. Weil die lokale Rissöffnung in Anhängigkeit der Spannungsintensität nicht ganz frei einsetzen kann, findet das Gesamtversagen erst nach einer Umverteilung der Spannungsintensität statt. Deshalb ist das ganzheitliche Versagen notwendigerweise von der Energie der Gesamtfläche des Risses abhängig und nicht von einer der örtlichen Großen. Für die geeignete Bauteilbewertung ist deshalb die Berücksichtigung von zwei Parametern nötig, die stellvertretend für die gespeicherte Energie sind: Spannung und Dehnung (Einschließlich der plastischen Verformungen) im kritischen Nettoquerschnitt mit dem Riss.
-
Ausgangsform eines Oberflächenrisses kann beliebig sein, aber unter der Ermüdungsbeanspruchung nimmt der Riss nach bestimmter zahl der Lastspiele die elliptische Kontur. Aus diesem Grund basieren alle bekannten analytische Lösungen an der Kontur der Ellipse mit den charakteristischen Parametern a und c.
-
In unseren experimentellen Untersuchungen haben wir festgestellt, dass die Darstellung der Ergebnisse basierend an den einzelnen Parameter der Ellipse und dem Verhältnis (a/c) zu größeren Streuung führt. Diese kann praktisch komplet ausgeschaltet werden (ausgenomen Einfluss der Plattendicken), falls als maßgebende Parameter die Flächen des Risses angenommen werden.
-
Um diese Abhängigkeit zu berücksichtigen, brauchen wir keine neuen analytischen Lösungen, da die Umstellung der bestehenden Lösungen sehr einfach ist. Das wird am Beispiel der meist verwendeten Lösung für Oberflächenriss in: STRESS-INTENSITY FACTOR EQUATIONS FOR CRACKS IN THREE-DIMENSIONAL FINITE BODIES SUBJECTED TO TENSION AND BENDING LOADS, by J. C. Newman, Jr. and I. S. Raju (NASA Technical Memorandum 85793, April 1984) gezeigt.
Ausgehend von

Schreiben wir
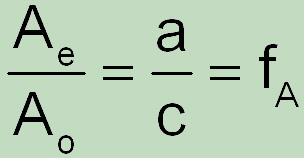
Faktor fA wollen wir mehr allgemein als „Flächenfaktor“ bezeichnen (und nicht als Formfaktor der Ellipse). Daraus folgt:
-
In wieweit die verschiedenen Abweichungen von der idealen elliptischen Form, die für die Praxis obwohl typisch sind in der Regel ignoriert werden, auf diese Weise erfasst werden können, könnte leider nicht untersucht werden. Allerdings zeigen die Untersuchungen von Chavla, D.S- at all in „The shape influence on the behaviour of surface crack” SMiRT 13, 1995 einen eindeutigen Trend in Abhängigkeit der Rissfläche und Form in diese Hinsicht.
-
Das Rissausbreitungspotenzial ist, im Einklang mit der Rissoberfläche, für rechteckige Crack maximal und für Dreiecksriss an Minimum. Allerdings, für dreieckige Riss die Spitze des Rissausbreitungspotenzials tritt nicht in der maximalen Tiefe auf, sondern etwas weg von dieser Lage. Daher, diese Art von Crack zeigt die Tendenz, unter Ermüdungsrissverlängerung in die ovale Form zu übergehen.
-
Die Veränderung der Restfestigkeit der angerissenen Struktur in Folge der zunehmenden plastischen Verformungen wird typischer weise in dem der sogenannten Failure Assessment Diagram (FAD) in Abhängigkeit von zwei Parametern dargestellt:
- Mehr allgemein ist die Versagenseinhüllkurve, basierend auf der J-Integral-Lösung, auf die folgende Weise definiert:
Kennzeichnenden Parameters der Rissgröße
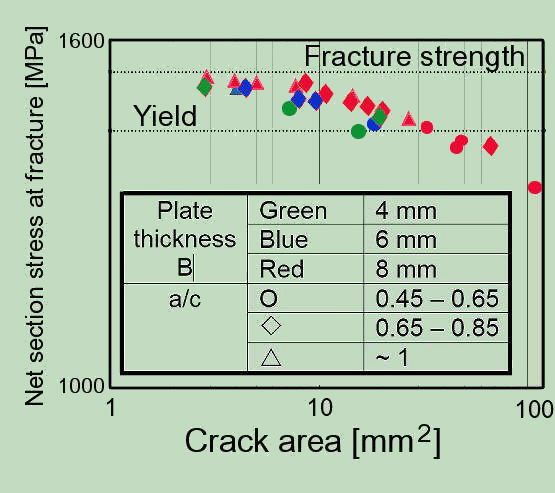

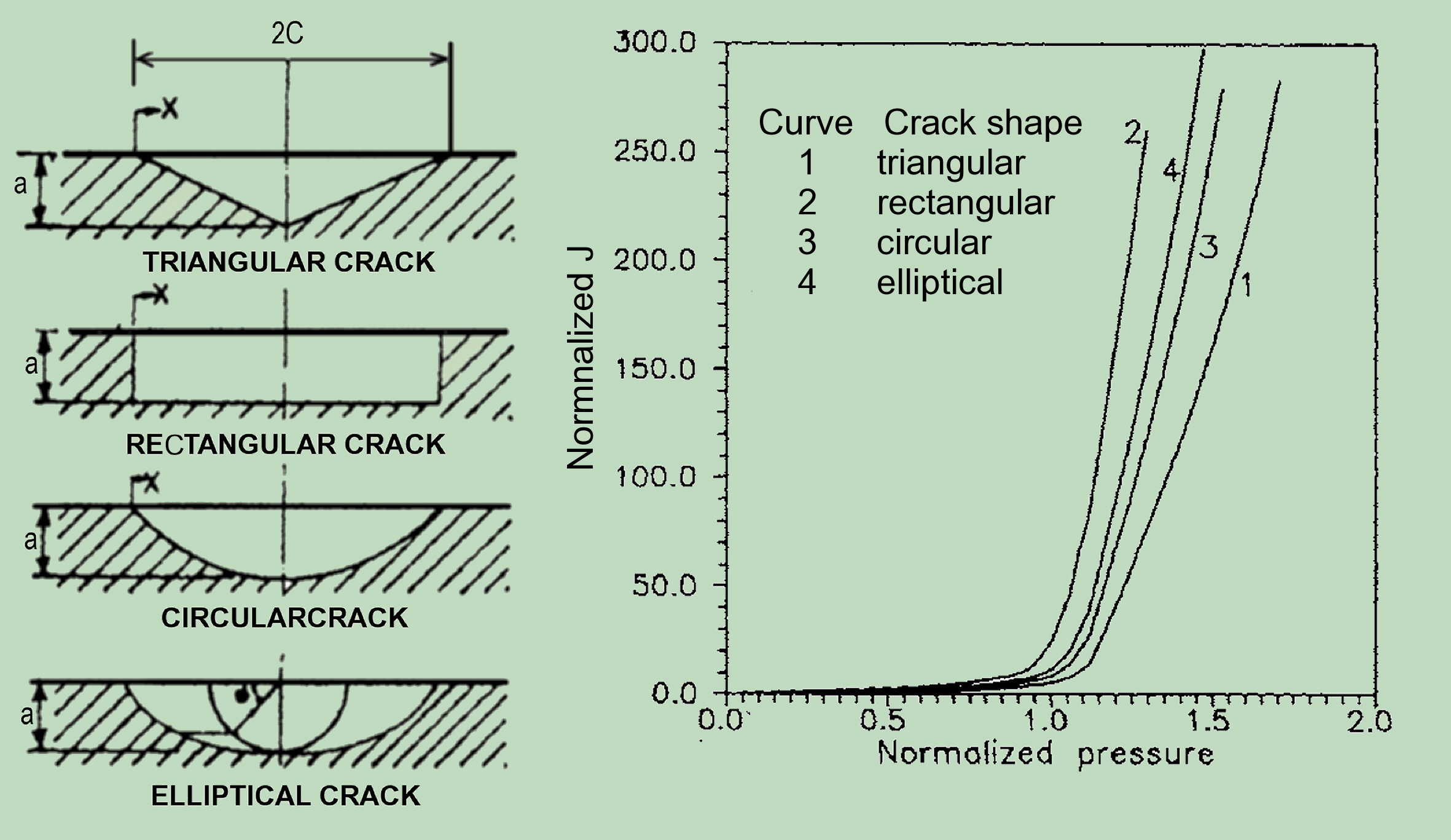
Vorstellung der neuen Methode und Nachweis ihren Vorteilen
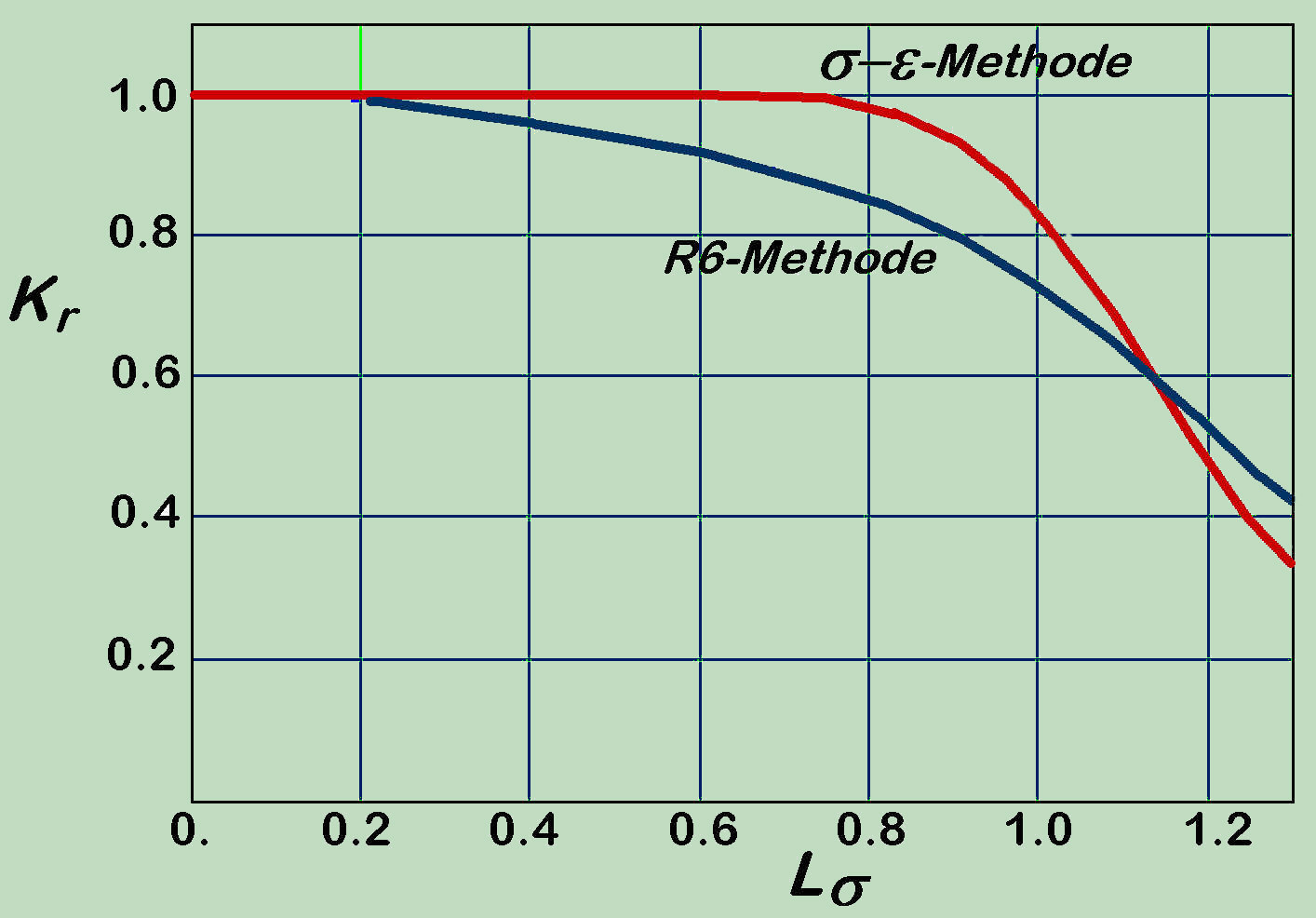
Kr.....Verhältnis des verringerten Spannungsintensitätsfaktors, KI beim Versagen und der Werkstoffbruchzähigkeit, Kmat
Lr.....Verhältnis der aktuellen Spannung und der Spannung, bei welcher die Fließgrenze des Werkstoffes überschritten wird, bzw. die plastischen Verformungen im kritischen Querschnitt die wesentliche Größe erreichen.

Während, aufgrund der bekannten LEBM-Beziehung für das J integral

gilt, liegt es nahe (in Anlehnung auf die Kerbnäherungsbeziehung nach Neuber) die gleiche Beziehung für die elasto-plastischen Bereich zu erweitern
Oder einfach:
![]()
Durch diese Erweiterung ergibt sich eine robuste Lösung, die in ganzem Bereich zwischen "elastisch" und "plastisch" verwendet, bzw. gelten wird. Durch mehrere FEM-Berechnungen wurde die Gültigkeit dieser Erweiterung untersucht und ohne Ausnahmen bestätigt.
Gesetzte der klassischen Plastizitäts-Theorie definieren die totalen Dehnung als summe der elastischen und der plastischen Komponenten mit den unabhängigen konstitutiven Beziehungen, die die beiden beschreiben. Deshalb wird auch der J-integral als summe der zwei Anteile geschrieben:
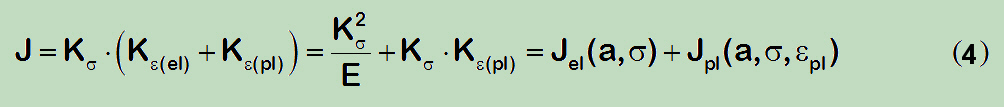
Wie zu feststellen ist, berücksichtigt der elastische Anteil des J-Integrals hier nicht die Irwin's Plastizitätskorrektur. Tatsächlich verfälscht diese Korrektur die Verhältnisse und ist deshalb nicht zu empfehlen. Bekanntlich sind duktile Werkstoffe imstande (aufgrund der Plastizität) die Effekte des Risses (oder Kerbe) zu reduzieren (Spannungsumverteilung, Abstumpfung), während die Irwin's Plastisch-Zone-Korrektur genau in die andere Richtung (Erhöhung der Rissgröße und dadurch den mehr erhöhten Spannungsintensitätsfaktor) geht. Für die zähen Werkstoffe ist diese Korrektur im Sinne einer Erhöhung der Rissgröße unangebracht. Obendrein, unter den Bedingungen der ebenen Dehnung ist diese Korrektur wesentlich kleiner als unter den Bedingungen der ebenen Spannung, womit der wichtigen Effekt der Dehnungsbehinderung sogar verfälscht wird.
Klar, bei Annäherung an die Streckgrenze wird der inelastische Anteil der Dehnung gegenüber elastischen bedeutsamer, sodass die entsprechende negativen Effekte, bzw. die J-Integralerhöhungsanteil an der Bedeutung gewinnt, was aber durch den zweiten Term in der Formel (4) berücksichtigt wird.
Anmerkung: Detaillierten Ableitungen aller Beziehungen findet Mann in den Literaturquellen, die am Ende des Textes angegeben sind!!!
Diese Ableitungen auch ergeben:

sodass aufgrund der üblichen exponenziellen Darstellung der stabilen kontinuierlichen Spannungs-Dehnungs-Kurve des Werkstoffes (σ = B.εpln) nach Ramberg-Osgood auch eine neue Beziehung für die FAD kurve bestimmt werden kann:
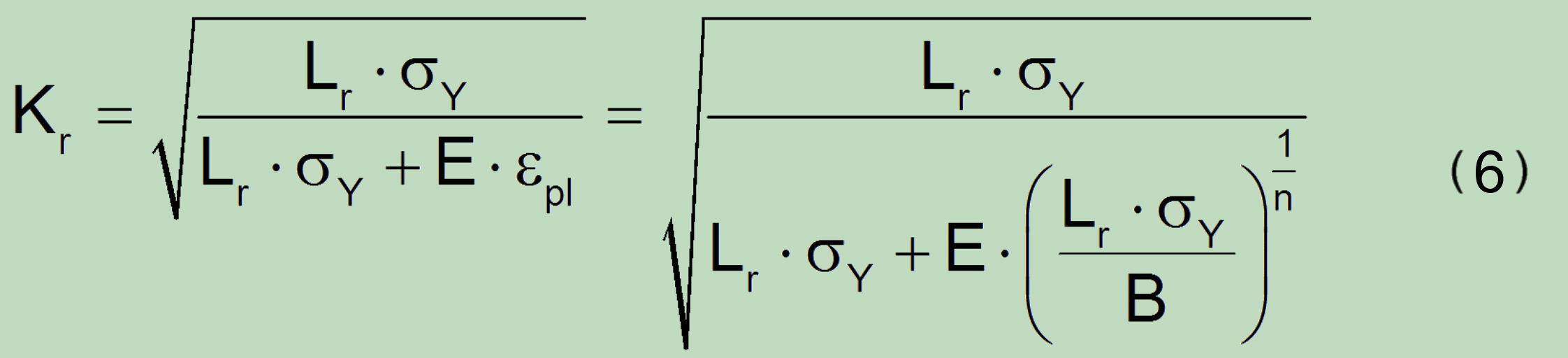
Dem gegenüber die bekannte R6 Beziehung:
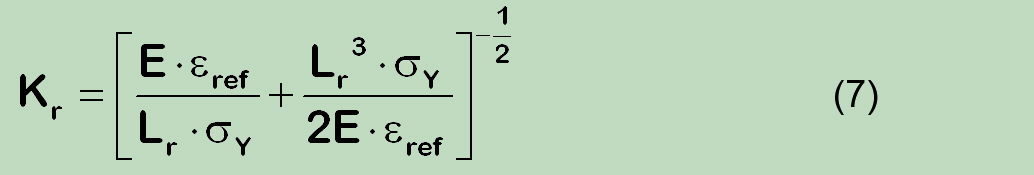
führt nachdem Umschrieben zu dem folgenden Ausdruck:
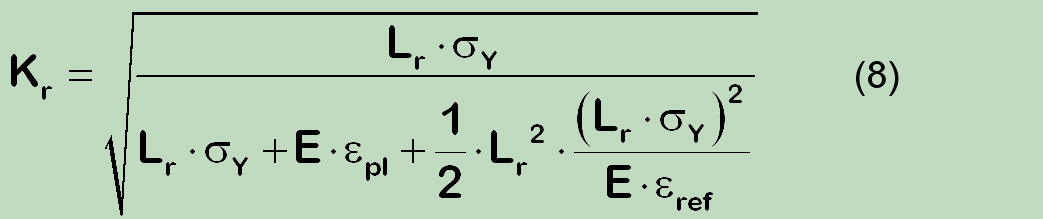
Im Verglichen zu der Beziehung (6), erscheint in dem Nenner der Bruchzahl ein Zusatzfaktor

Der Herkunft dieses Unterschiedes kann man ableiten unter der Berücksichtigung, dass, wenn die Spannung im Nettoquerschnitt die Streckgrenze erreicht hat, der erste Term = 1 ist, sodass folgt

Das heißt, diese Beziehung ist nur an der Berücksichtigung von PZ Korrektur gebunden, die in der gegebener Form sogar die Effekte der Dehnungsverfestigung ausschließt.
Die zusätzliche Erhöhung des plastischen Anteils des J-Integrals (8) zur Konstruktion des FADs (R-6, SINTAP, etc.) basiert, außerdem auf dem inhomogenen Verhältnis:
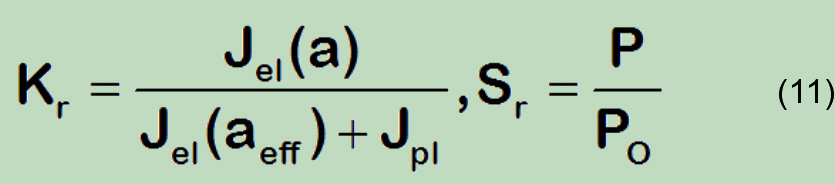
Wie bereits festgestellt (sieche Details oben) hat die PZ- Korrektur keinen plausiblen theoretischen Hintergrund und ist zur Anwendung auf zähen Ingenieur-Werkstoffe kontraproduktiv. Im übrigens beim einsetzten der Nonlinearität der exponentiellen Spannungs-Dehnungskurve (bereits unterhalb der Streckgrenze) erfolgt die Korrektur durch die Beträge der plastischen Dehnung εpl in dem durch Riss geschwächten Querschnitt. Gleichvoll, bei Lr ≥ 1 ist die plastische Zone = gesamte kritische Querschnitt und die Verwendung diese Korrektur zur Bestimmung der „effektiven“ Rissgroße hat kaum ein Sinn mehr.
Folglich muss der zweite Argument in (7) Im Bereich Lr ≥ 1 gestrichen werden.
Die Anwendung von (6) schlisst die PZ-Korrektur nicht zwingend aus. Diese kann bei der Berechnung von K für die aktuelle Geometrie natürlich berücksichtigt werden, wobei die Anwendung von mehr sinnvollen Beziehung (Shih, et al.), die auch die Verfestigungseinflüsse berücksichtigt zu empfehlen ist:
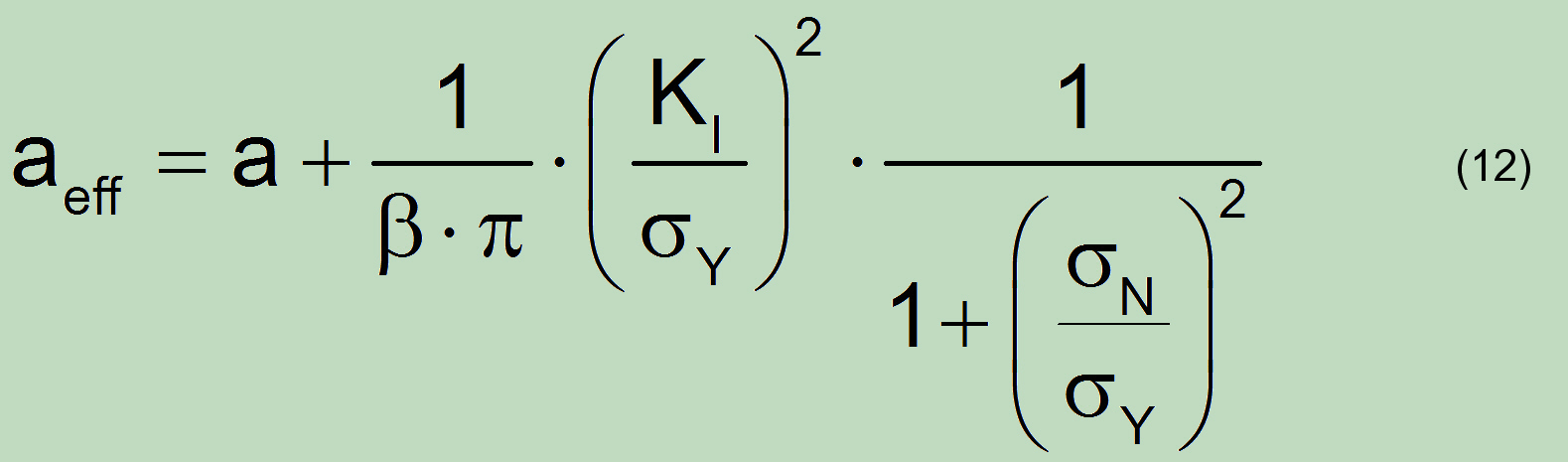
Nachweis der neuen Methode
Die vorgeschlagene Spannungs-Dehnungs-Methode ist durch zahlreiche Versuche (die auch an bauteilähnlichen Körper durchgeführt wurden) für die Anwendung an den kritischsten dünnwandigen Komponenten mit oberflächlichen Fehlern nachgewiesen.


Das nachfolgende Diagramm bestätig denselben Trend, wie bei dem vorangehenden FAD-Vergleich. Die Übereinstimmung mit den experimentellen Ergebnissen ist für die vorgeschlagene Methode perfekt. Im Falle von R-6/Option 2 dagegen, deuten die Ergebnisse auf eine systematische Abweichung gegenüber den experimentellen Ergebnissen, die in dem Formelaufbau des FADs von R-6/Option 2 liegt und die Notwendigkeit einer Plastic Zone Korrektur, wie in (12) infrage stellt.
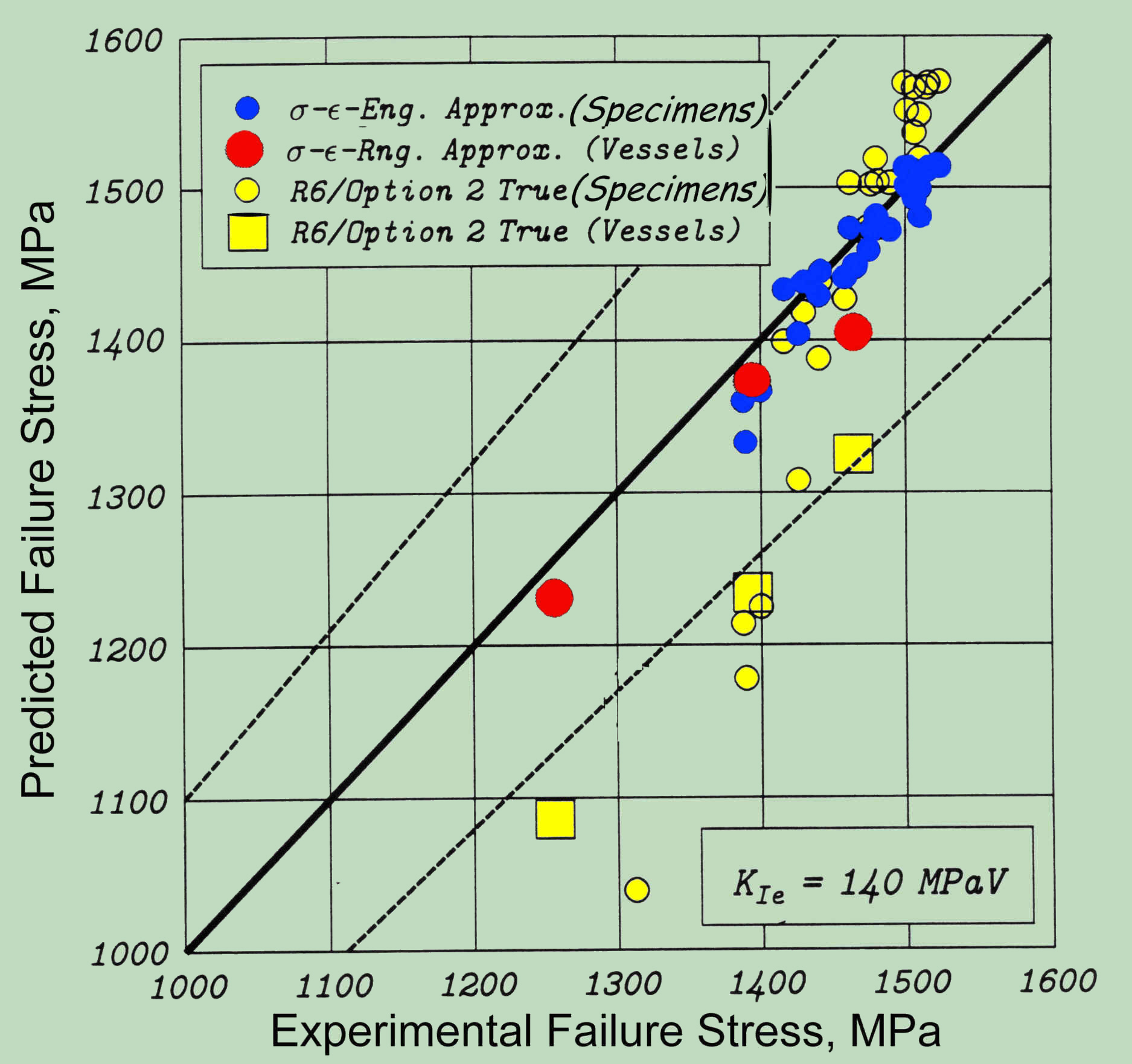
Erhöhte Genauigkeit der hier vorgeschlagenen Methode im Vergleich zu den bestehenden Methoden (R-6, FAD, etc.), sowohl unterhalb als auch oberhalb der Streckgrenze vermeidet den unnötigen Konservativismus bei der Auslegung in diesem für die Anwendungen wichtigsten Bereich.
und für die Veröffentlichung (in engl.):
Development of residual strength evaluation tool based
on stress-strain approximation, in Int. Journ. of Fracture 88 (1997) pp. 129 -152 (leider Gebühren pflichtig), oder
Proposal for the Improved Design of Reliable
Failure Assessment Diagrams for Components with Surface Crack, in Structural Integrity and Life Vol. 13, No2(2013)
pp. 99 - 108 (free)
Zum Abschluss noch eine Anmerkung !
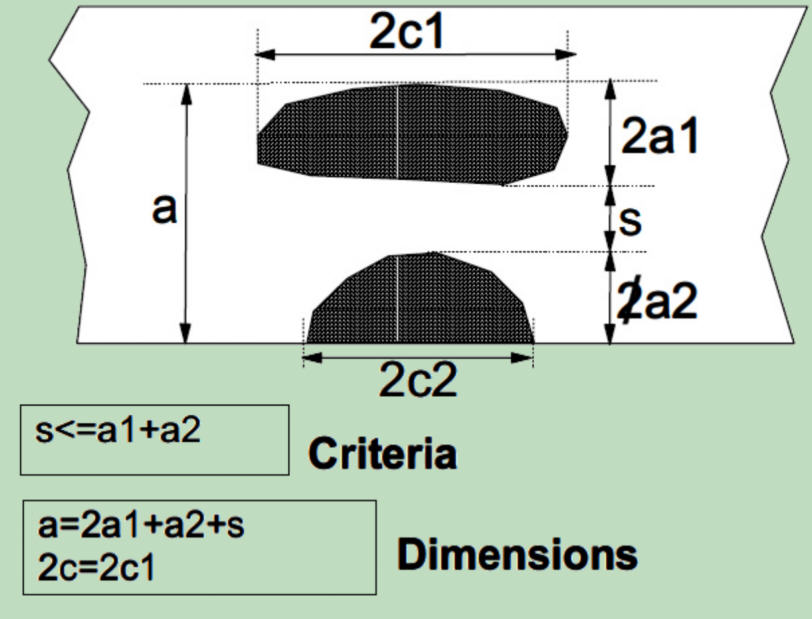
Leider sind im SINTAP auch andere Schwächen von den bisherigen Standards auch unbedacht übernommen, wie zum Beispiel zur Behandlung der Rissinteraktion.
In keinem der Fälle werden die Rissschließeffekte des Materials zwischen beiden Grundrissen berücksichtigt, die natürlich mit der Erhöhung von s auch verstärken. Die Folge ist, immer wenn s kleiner ist (Schließeffekte auch kleiner), soll der resultierende Riss als weniger gefährlich (?) bewertet werden. Auf der anderen Seite für den Fall s = a1 + a2 erreicht der Ersatzriss seine maximalle Größe obwohl gleich danach (s > a1 + a2) die Interaktion der beiden Risse vernachlässigt werden soll. Einen vernünftigen Übergang fehlt komplett aus.
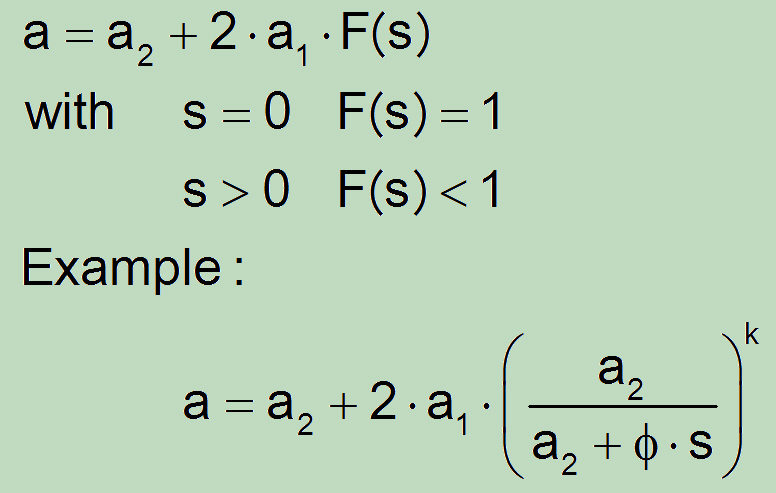
Eine geeignete Beziehung kann, zum Beispiel, die folgende Form haben:
Allerdings, für einen sachlichen Vorschlag diesbezüglich fehlen, bedauerlicherweise zur Zeit verlässliche experimentelle und/oder numerische Untersuchungen.
Zurück zum AnfangZurück zur Hauptseite