Unlike to the original linear model, for taking into account nonlinear damage accumulation effects based on experimental evidence, the critical value of fatigue-creep damage D is in the actual codes not specified as a constant equal to 1 but as a variable dependent on the creep and fatigue damage fractions and actual material. The corresponding bi-linear dependence is given graphically in the form of a creep-fatigue interaction envelope. The various envelope lines given in the current codes restrict the use of different materials to extremely low values (0.02, 0.1), making them not only difficult to put into practice but also especially unsuitable for modern constructions and materials!
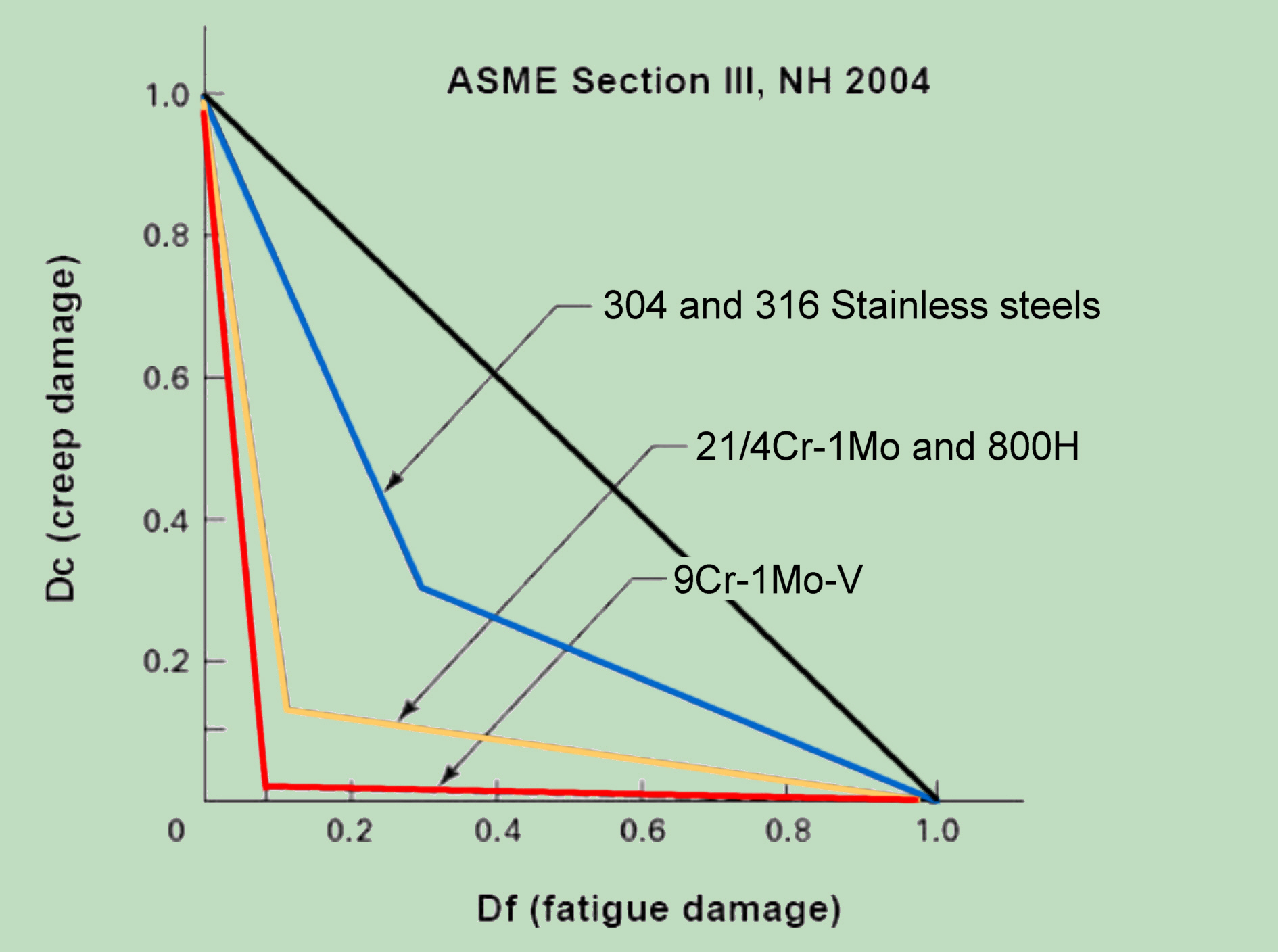
These extreme shortcomings indicate the existence of additional mechanisms that enhance the entire damage process and reduce life under creep fatigue interaction conditions. It is misleading to contemplate that, with high reserve factors, even after their "statistical assurance". In opposite, as the operating temperature increases, these additional mechanisms dominate the damage process and, if not properly considered, may limit the successful design and material application unintentionally high.
Consideration of the oxidation using Time-Temperature-Substitution-Factor (TTSF)
-
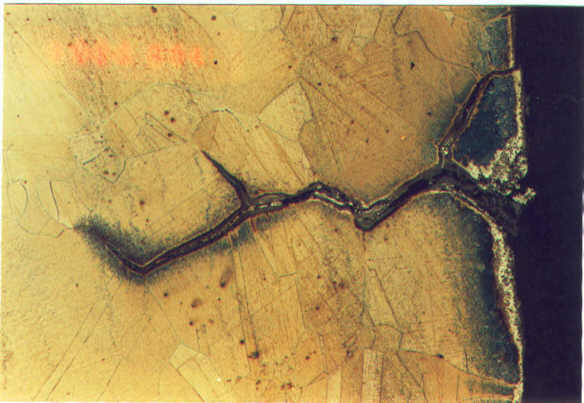
Our investigations for creep-fatigue loading conditions at very high temperature (850 °C) with the Alloy 800H have shown that the addition of a tensile hold time at maximum load to a fatigue cycle tends to significantly reduce the lifetime. Grain boundary chemistry (Figure) is shown to be a significant factor that considerably affects strengthening, weakening and damage behaviour of austenitic stainless steels and nickel-base alloys. Due to the grain boundary oxidation, which penetrates deeper than surface oxidation, accelerated fatigue crack nucleation (or "damage incubation") has appeared and a significant shortening in the lifetime of the cyclic dwell tests is found. Oxidation also accelerates fatigue damage both in terms of fatigue crack initiation and fatigue crack propagation. Once initiated, the cracks which open under the load, thus expose the new deeper surface layers to the gas phase and oxidation.
-
The advanced method was firstly developed based on the improvement of the classical Strain Range Partition Method and successfully tested within the framework of the BRITE project P 1209. The developed method uses a synergy between simplified, but robust, design rules for high-temperature systems based on consideration of time-dependent material properties and accelerated material characteristics testing.
-
The phenomenological basis of the SRP-method can be represented as follows: During holding periods and time-dependent stress change, in addition to plastic deformation (P) relevant creep (C) strains are occurring. Simultaneous creeping at tension and pressure side of closed cycle results in CC-strain partition. The within one cycle not balanced creep strains yield either CP or PC partitions, why within a same load loop just either tension or pressure partitions can occur as a result of creep and plastic strain blend. Due to oxidation and tension influences, the CP partition affects more the lifetime. It should be noted in particular that the oxidation very strongly accelerated the formation of cracks on surfaces and in this way strongly reduce the PP portion of the life time. Original SRP method ignore this.
-
As can be seen, the SRP test forms are based on the simplifications that are not representative for the stress-strain history of components. Further examples of the CP load effects in the laboratory are with hold times at the constant strain in tension, which, however are also less consistent with the loading histories in practice. In addition, the laboratory tests carried out are usually of short duration, on the order of several hours to several hundred hours. Components operating at high temperatures, should be designed for several thousands of hours or even hundreds of thousands of hours. Therefore, if creep-fatigue data generated in the laboratory at short times are extrapolated to the practical long life, the time dependence of the lifetime relationships should be taken into account.
-
Up to now two modifications of the SRP method have been proposed for this purpose, developed in approximately the same time as our project (1986). By steady-state creep rate (SSCR) and Exposure Time (ET) modified CP-life relationship characterize the influence of the total amount of time (up to failire) on the CP strainrange by assuming that the PP-life relationship is not time dependent. For the determination of the PP life relations the strain controlled experiments with relatively high frequency are used, which results in very little time of the corresponding experiments, for the cyclic life to be deteriorated by oxidation or metallurgical instability. Microstructural characterization shows however that the time effects that are observed, must have the impact on the PP strainrange, because this pation represents pure fatigue, which is in total more sensitive to the grain boundary oxidation than CP should be. Thus, when PP strain partitioning occurs in combination with CP or PC, the time effect to the PP strainrange should be not only not to neglect, but also to consider as the decisive factor.
-
To take into account the effects of the enbrittled surface layers, aroused through the oxidation that penetrates alongside the grain boundaries, on the crack initiation, we introduce a correction into the known Strain Range Partitioning method, which is then in the case of the tensile relaxation dwell determined by the relationship:
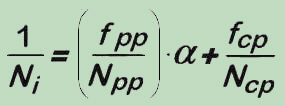
Note that the correction relates solely to the reduction of fatigue life or respectively crack formation on the surfaces. Herein, the correction-factor (α) can be represented through the relation known as the Arrhenius-Equationn, that takes into account the interdependence dependence of the temperature and time
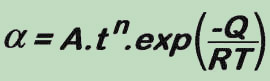
-
In this way, similar to pure fatigue, the development of the damage at the critical point will be determined, even though the concept of so-called crack initiation would be less appropriate. It was found, for example, in our experiments that the creep strains during the dwell after the period of stable (steady state) growth receives the over-linear character leading to the rapid failure of the samples, which is a consequence of creep damage (porosity) in the whole volume of the specimen. To distinguish this phase, in which, besides the formation of cracks at the enbrittled surface at the same time the damage in the whole volume of material takes place, is characterized more generally as the damage incubation.
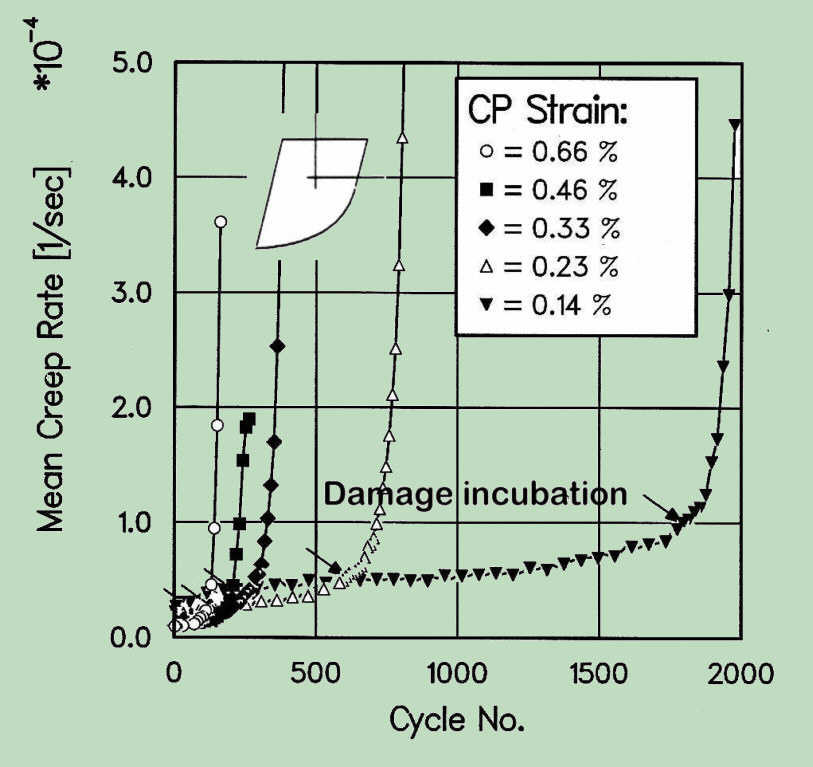
-
In practice, at a critical area (the notch root or else) under creep-fatigue conditions considerable stress redistribution occurs due to the inelastic strains and this alters the stress-strain history changes from that expected based on the linear stress strain analysis. Clearly, the corresponding conditions can be evaluated by full nonlinear structural analysis (visco-plastic); however, this can be very expensive and time consuming. For this reason, especially in the preliminary design of components, an approximate procedure for predicting the inelastic stress-strain history is used.
-
If one compares the stress-strain history, predicted according to well-known Neuber hyperbola approximation, with that of a typical creep-fatigue test with the strain hold during dwell time, it is evident that the approximation does not hold. At the same time, as the figure shows, the results obtained applying the Neuber approximation may be too conservative.
-
The above observations show that another kind of test and approximation basis are necessary which can be better adapted to creep-fatigue conditions. For this reason, we have introduced a "generalized" Neuber hyperbola equation with a variable exponent "n":
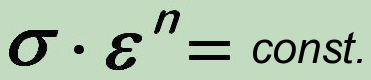
This allows very different histories to be accounted for by varying the n-value between zero (constant stress) and ∞ (constant strain).
-
In addition, the lifetime after damage incubation is significantly reduced. When the creep damage is immensely advanced in the material volume, the subsequent crack propagation would be also greatly accelerated.
-
The simple accumulation of fatigue and creep damage (without their interaction effects) may seriously underestimate these combined effects. If well understood, it could also be possible to control all effects by proper design.
-
To compensate for the deficiencies of the previous methods of lifetime prediction, as already indicated, even by recognized codes, very high (Un)safety margins are demanded. In this way, in addition to the actual scattering effects, the natural influences, which are not taken into account, should also be covered. Due to its stiff nature, this approach is very limited in its usefulness for the consideration of the dynamic changes of the relevant factors.
-
Traditional life analysis involves analysing times-to-failure data obtained under normal operating conditions to quantify the life characteristics of the product, system or component. In many situations, and for many reasons, such life data (or times to-failure data) is very difficult, if even impossible, to obtain.
-
Therefore, to meet increasing competition, get products to the market in the shortest possible time, and satisfy customer expectations, traditional test methods are no longer sufficient .
-
Given this difficulty, and the need to observe failures of products to better understand their failure modes and their life characteristics, design practitioners have attempted to devise methods to force these products to fail more quickly than they would under normal use conditions (accelerated test sequence). In other words, they have attempted to accelerate their failures. Over the years, the term accelerated life testing has been used to describe all such practices.
-
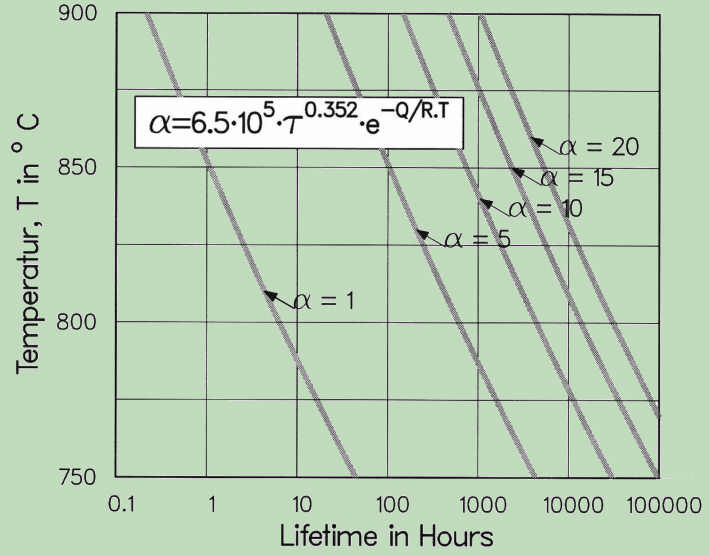
Based on the Zeit-Temperatur-Substitutions-Faktor (ZTSF) this kind of life management can be successfully applied. The following diagram shows that for equal inelastic strain range, the increase in temperature for 60 °C allows the reduction of the test duration, from 10000 to 1000 hours. If the number of cycles in this case has to be unchanged, the dwell time should be reduced according to the time reduction factor. The method can help to reduce the amount of experimental effort in the design of components for operation under creep-fatigue conditions and their optimisation and efficient redesign.
-
The actual transient events occur over a temperature range. In contrast to this the current code rules and the available methods are based on isothermal data. Because of this there are also differences of opinion relative to the use of isothermal data for predicting transient events.
-
The above Alfa-relationship represents a correction as the function of time and temperature. Based on this the proposed model is fully suitable under non-isothermal conditions, i.e. for the purposes of thermal-mechanical creep-fatigue evaluation. The actual transients can be considered integrating the equation (α) according to the temperature change in time
-
If the temperature history is dominated by a limited number of different levels the resulting correction factor equals the sum:
-
In case of lifetime prediction the final results (Ni) should usually be produced by iteration.
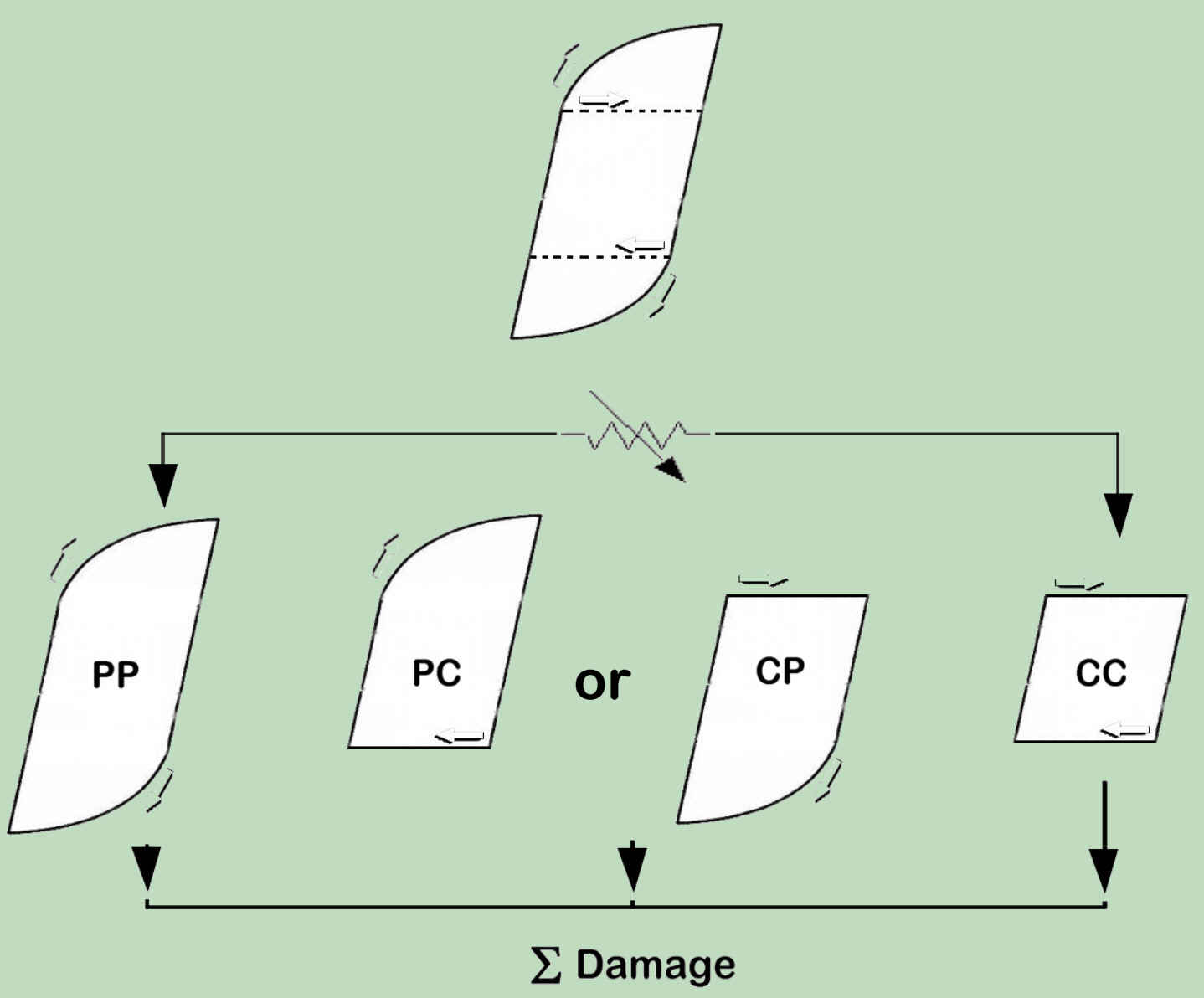
Method that fully considers both: oxidation effects and components load history (using corresponing correction factors α and p) is established in P-1209 project and verified by the tests:
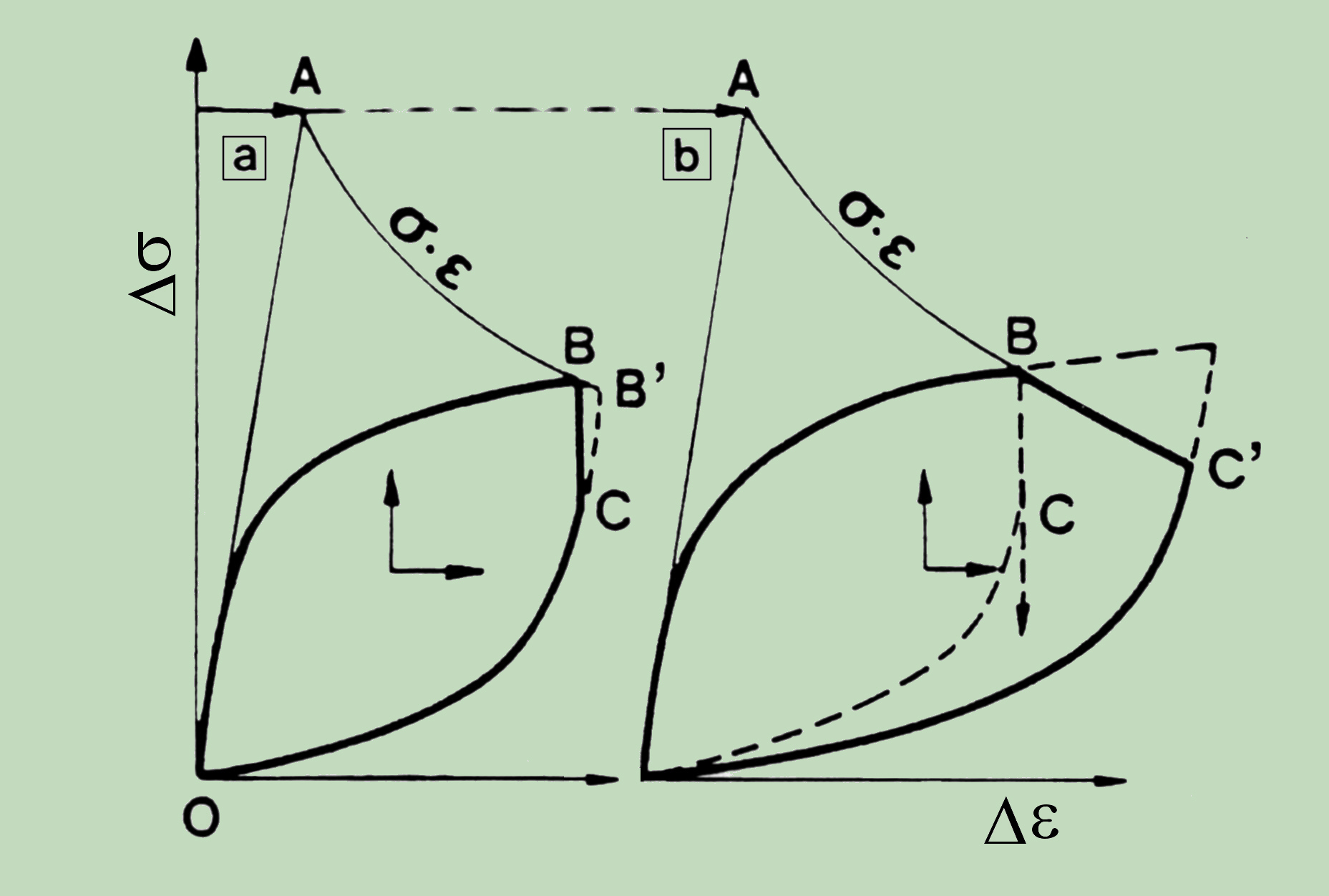
Verification of the method
The proposed method was verified with help of own experimental examinations and the results of examination from the literature, that refers to the conditions with dwell time under tensile loading with the same material (IN 800H). In this way, also the numerous influences of the material-charges, heat treatment and test-conditions has been fully included. At the same time the amounts which relate to inadequate methods of calculation set were sorted out of the natural scatter and with it the resulting scatter reduced to the real random effects. The following comparison shows an excellent result, both in terms of accuracy of predictions as well as in respect to the improvements of the original method:
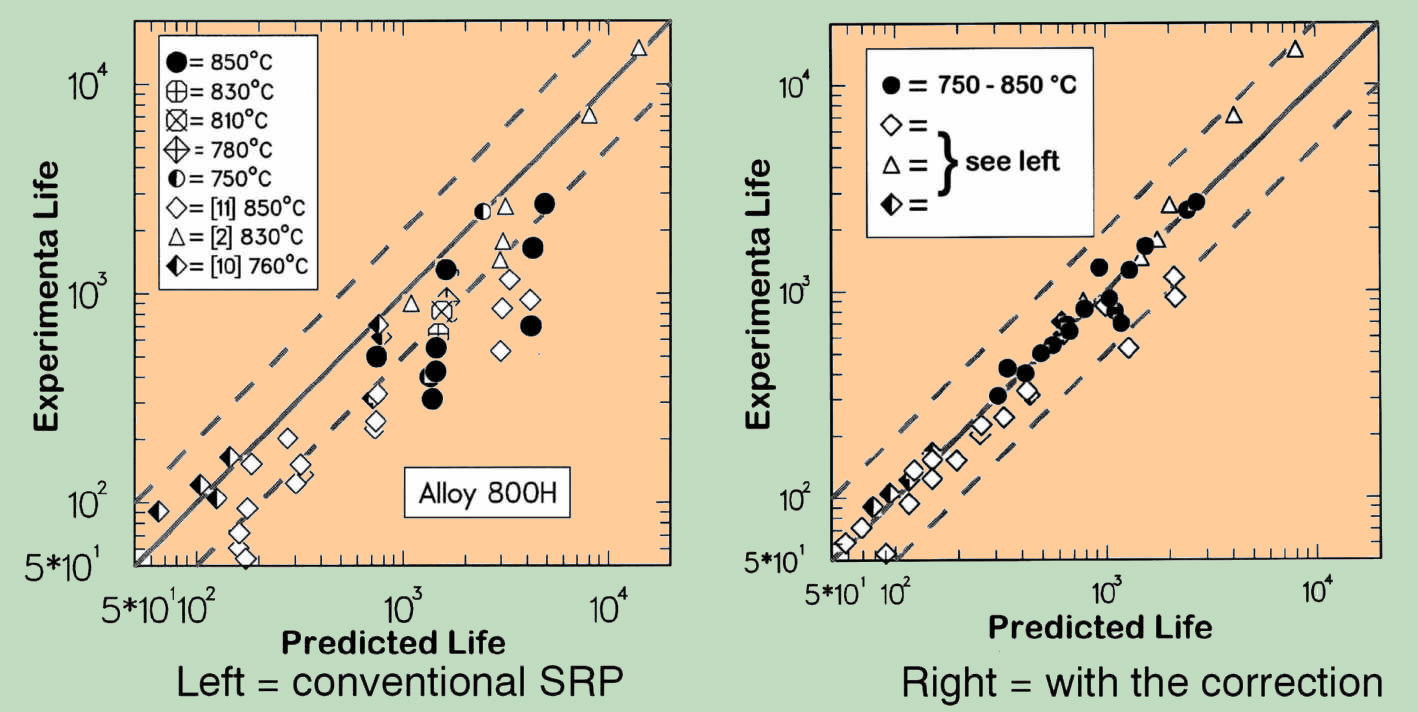
Based on the results of the project, several useful prerequisites for successful application have been created for the better understanding of the behavior and the effective design of high temperature components:
Safety factors that only consider the statistically sizeable 'natural' scatter (and based on this may be better controlled)
Accelerated lifetime testing
Application under thermal transients and
thermo-mechanical load conditions
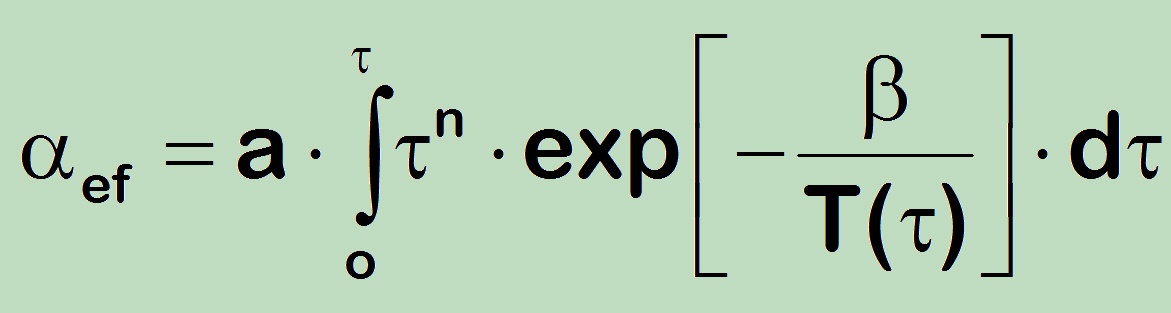
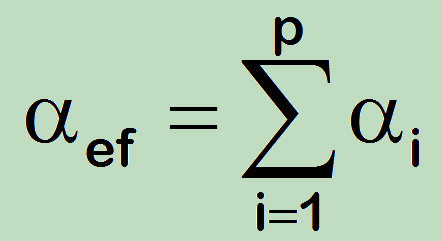
Back to the beginning
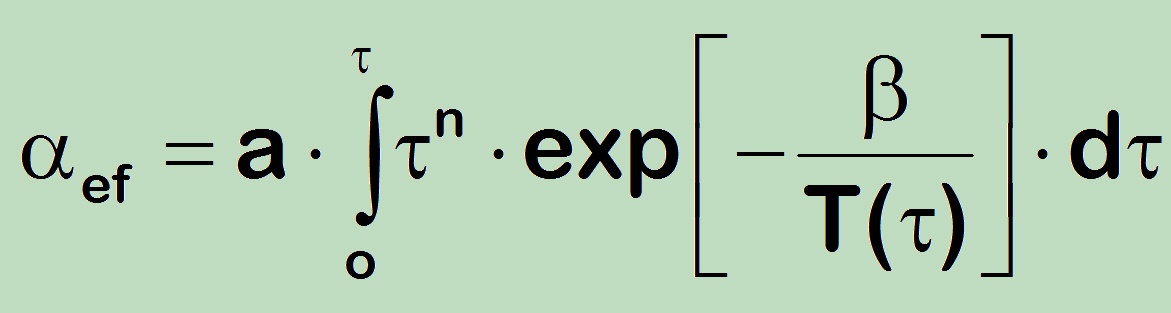
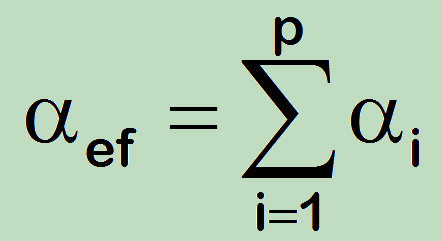
More details you can find in the above-cited paper and in:
It is my hope that both papers will help to clarify some of the problems that still remain to be treated.
Return to topReturn to main page
